MATLAB - 逆傅里叶变换

上一页
下一页

MATLAB 中的逆傅里叶变换是一个函数，它接收信号的频域表示，并将其转换回时域表示。它是傅里叶变换的反向过程，傅里叶变换将时域信号转换为其频域表示。

在 MATLAB 中，逆傅里叶变换使用 `ifft` 函数（对于一维信号）和 `ifft2` 函数（对于二维信号）计算。逆傅里叶变换的结果是代表原始时域信号的信号。

逆傅里叶变换在信号处理、图像处理和通信中非常有用，它用于分析和处理频域中的信号。它允许对频域中表示的信号执行诸如滤波、压缩和调制之类的操作。

使用 `ifft()` 进行逆傅里叶变换

MATLAB 中的 `ifft()` 函数计算序列的逆离散傅里叶变换 (IDFT)。它接收表示频域信号的一维或二维数组（例如，使用 `fft()` 函数获得），并返回相应的时域信号。

逆离散傅里叶变换是离散傅里叶变换 (DFT) 的逆过程。它将信号的频域表示转换回时域表示。这在需要在频域中分析或处理信号，然后将其转换回时域以进行进一步处理或解释的应用中非常有用。

语法

X = ifft(Y)
X = ifft(Y,n)
X = ifft(Y,n,dim)
X = ifft(___,symflag)

语法解释

X = ifft(Y) 使用快速算法计算 Y 的逆傅里叶变换。结果 X 与 Y 大小相同。

  • 如果 Y 是向量，`ifft(Y)` 返回向量的逆变换。
  • 如果 Y 是矩阵，`ifft(Y)` 返回矩阵每一列的逆变换。
  • 如果 Y 是多维数组，`ifft(Y)` 将沿第一个非单一维度上的值视为向量，并返回每个向量的逆变换。

X = ifft(Y,n) - 计算 Y 的逆傅里叶变换，但在执行变换之前，用零填充 Y 以使其长度为 n。

X = ifft(Y,n,dim) - 沿指定的维度 dim 计算 Y 的逆傅里叶变换，用零填充以沿该维度使长度为 n。例如，如果 Y 是矩阵，`ifft(Y,n,2)` 计算每一行的 n 点逆变换。

X = ifft(___,symflag) - 允许您指定 Y 的对称性以及任何之前的输入参数组合。例如，`ifft(Y,'symmetric')` 将 Y 视为共轭对称。

MATLAB 中逆傅里叶变换的示例

让我们看看上面提到的每种语法的示例。

示例 1：使用 `ifft(Y)` 计算逆傅里叶变换

我们的代码如下：

% Generate a signal
t = linspace(0, 1, 1000); % Time vector
f = 5; % Frequency of the signal
signal = sin(2*pi*f*t);

% Compute the Fourier Transform
Y = fft(signal);

% Compute the Inverse Fourier Transform
X = ifft(Y);

% Plot the original and reconstructed signals
subplot(2,1,1);
plot(t, signal);
title('Original Signal');
xlabel('Time');
ylabel('Amplitude');

subplot(2,1,2);
plot(t, real(X)); % Display real part of X
title('Reconstructed Signal');
xlabel('Time');
ylabel('Amplitude');

在这个例子中：

  • 我们首先生成一个正弦信号 signal。
  • 然后我们使用 `fft()` 计算信号的傅里叶变换，结果为 Y。
  • 接下来，我们使用 `ifft(Y)` 计算逆傅里叶变换，理想情况下应该重建原始信号。
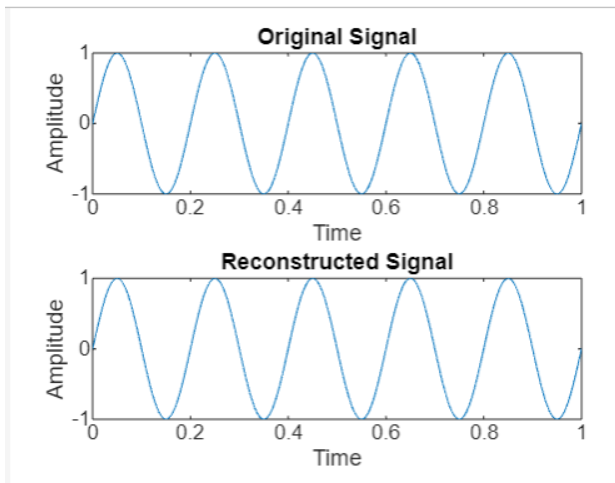
  • 最后，我们绘制原始信号和重建信号以进行比较。

代码执行后，我们得到以下输出：

示例 2：计算具有零填充的逆傅里叶变换

我们的代码如下：

% Generate a signal
t = linspace(0, 1, 1000); % Time vector
f = 5; % Frequency of the signal
signal = sin(2*pi*f*t);

% Compute the Fourier Transform
Y = fft(signal);

% Compute the Inverse Fourier Transform with zero padding
n = 2000; % Length to pad
X = ifft(Y, n);

% Plot the original and padded signals
subplot(2,1,1);
plot(t, signal);
title('Original Signal');
xlabel('Time');
ylabel('Amplitude');

subplot(2,1,2);
t_padded = linspace(0, 1, n); % Time vector for padded signal
plot(t_padded, real(X)); % Display real part of X
title('Padded Signal');
xlabel('Time');
ylabel('Amplitude');

此示例类似于前一个示例，但增加了零填充。

  • 在计算信号的傅里叶变换之后，我们使用 `ifft(Y, n)` 计算具有零填充到长度 n 的逆傅里叶变换。
  • 零填充可用于提高信号频域表示的分辨率。

执行后的输出为：

示例 3

沿特定维度计算具有零填充的逆傅里叶变换

我们的代码是：

% Create a 2D matrix
A = magic(4); % Magic square matrix
disp('Original Matrix:');
disp(A);

% Compute the Fourier Transform along the columns
Y = fft(A, [], 2);

% Compute the Inverse Fourier Transform along the columns with zero padding
n = 8; % Length to pad
X = ifft(Y, n, 2);

% Display the original and padded matrices
disp('Original Matrix after IFFT along columns with zero padding:');
disp(X);

在这个例子中：

  • 我们从一个 4x4 的幻方矩阵 A 开始。
  • 然后我们使用 `fft(A, [], 2)` 计算 A 沿列的傅里叶变换，结果为 Y。
  • 接下来，我们使用 `ifft(Y, n, 2)` 计算沿列具有零填充到长度 n 的逆傅里叶变换。
  • 结果 X 是一个 4x8 的矩阵，其中每一行都是原始矩阵 A 中对应行的 n 点逆变换。

执行后的输出如下：

>> % Create a 2D matrix
A = magic(4); % Magic square matrix
disp('Original Matrix:');
disp(A);

% Compute the Fourier Transform along the columns
Y = fft(A, [], 2);

% Compute the Inverse Fourier Transform along the columns with zero padding
n = 8; % Length to pad
X = ifft(Y, n, 2);

% Display the original and padded matrices
disp('Original Matrix after IFFT along columns with zero padding:');
disp(X);

Original Matrix:
   16    2    3   13
    5   11   10    8
    9    7    6   12
    4   14   15    1
Original Matrix after IFFT along columns with zero padding:
 Columns 1 through 4:

   8.0000 +      0i   4.2500 + 4.7426i   1.0000 +      0i   4.2500 - 0.1464i
   2.5000 +      0i   4.2500 - 1.9142i   5.5000 +      0i   4.2500 + 0.1464i
   4.5000 +      0i   4.2500 + 0.9142i   3.5000 +      0i   4.2500 + 0.1464i
   2.0000 +      0i   4.2500 - 3.7426i   7.0000 +      0i   4.2500 - 0.1464i

 Columns 5 through 8:

   1.5000 +      0i   4.2500 - 3.7426i   6.5000 +      0i   4.2500 - 0.8536i
   5.0000 +      0i   4.2500 + 0.9142i   4.0000 +      0i   4.2500 + 0.8536i
   3.0000 +      0i   4.2500 - 1.9142i   6.0000 +      0i   4.2500 + 0.8536i
   7.5000 +      0i   4.2500 + 4.7426i   0.5000 +      0i   4.2500 - 0.8536i

>>

示例 4：计算具有指定对称性的逆傅里叶变换

我们的代码如下：

% Create a complex signal
t = linspace(0, 1, 1000); % Time vector
f = 5; % Frequency of the signal
signal = exp(1i*2*pi*f*t); % Complex exponential signal

% Compute the Fourier Transform
Y = fft(signal);

% Compute the Inverse Fourier Transform with symmetric treatment
X = ifft(Y, 'symmetric');

% Plot the real part of the original and reconstructed signals
subplot(2,1,1);
plot(t, real(signal));
title('Original Signal (Real Part)');
xlabel('Time');
ylabel('Amplitude');

subplot(2,1,2);
plot(t, real(X)); % Display real part of X
title('Reconstructed Signal (Real Part)');
xlabel('Time');
ylabel('Amplitude');
  • 在这个例子中，我们使用带有 'symmetric' 标志的 `ifft` 函数来指定输入信号的对称性。
  • 我们首先创建一个复指数信号 signal 并计算其傅里叶变换。
  • 通过使用 `ifft(Y, 'symmetric')`，我们计算具有对称处理的逆傅里叶变换，这假设输入信号是共轭对称的。
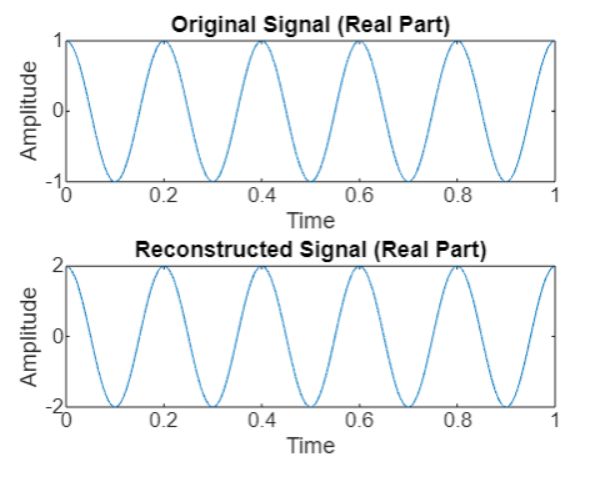
  • 绘制原始信号和重建信号的实部以进行比较。

执行后我们得到的输出如下：

使用 `ifft2()` 进行二维逆傅里叶变换

使用 `ifft2()` 进行二维逆傅里叶变换是一个 MATLAB 函数，它计算二维矩阵的逆傅里叶变换。它是二维傅里叶变换的逆运算，将图像的频域表示转换回空间域。

此函数在图像处理中特别有用，用于图像重建、滤波和恢复等任务。它接收表示频域图像的二维矩阵，并返回相应的空间域图像。

语法

X = ifft2(Y)
X = ifft2(Y,m,n)
X = ifft2(___,symflag)

语法解释

X = ifft2(Y) - 使用快速算法计算矩阵 Y 的二维逆傅里叶变换。如果 Y 是多维数组，`ifft2` 将计算高于 2 的每个维度的二维逆变换。输出 X 与 Y 大小相同。

X = ifft2(Y,m,n) − 通过截断或用零填充 Y 来将其大小调整为 m×n 矩阵，然后再计算逆变换。输出 X 也是 m×n 的。如果 Y 是多维数组，则 ifft2 会重塑 Y 的前两个维度以匹配 m 和 n。

X = ifft2(___,symflag) − 除了任何之前的输入参数组合之外，还可以指定 Y 的对称性。例如，ifft2(Y,'symmetric') 将 Y 视为共轭对称。

让我们根据上面提到的语法，来看几个例子。

示例 1：计算二维逆傅里叶变换

我们的代码如下：

% Compute the 2D Fourier Transform
Y = fft2(A);

% Compute the Inverse Fourier Transform
X = ifft2(Y);

% Display the original and reconstructed matrices
disp('Original Matrix:');
disp(A);

disp('Reconstructed Matrix:');
disp(X);
  • 此示例演示如何使用 ifft2() 计算矩阵 Y 的二维逆傅里叶变换。
  • 我们从一个简单的 3×3 矩阵 A 开始。
  • 然后，我们使用 fft2() 计算 A 的二维傅里叶变换，结果为 Y。
  • 最后，我们使用 ifft2(Y) 计算逆傅里叶变换，理想情况下应该重建原始矩阵 A。
  • 显示原始矩阵和重建矩阵以进行比较。

执行后，我们得到：

Original Matrix:
     1     2     3
     4     5     6
     7     8     9

Reconstructed Matrix:
     1     2     3
     4     5     6
     7     8     9

示例 2：调整二维逆傅里叶变换的大小

我们的代码如下：

% Create a simple 3x3 matrix
A = [1 2 3; 4 5 6; 7 8 9];

% Compute the 2D Fourier Transform
Y = fft2(A);

% Adjust the size and compute the Inverse Fourier Transform
m = 4; % Desired number of rows
n = 5; % Desired number of columns
X = ifft2(Y, m, n);

% Display the original and adjusted-size matrices
disp('Original Matrix:');
disp(A);

disp('Adjusted-size Matrix:');
disp(X);
  • 此示例说明如何使用 ifft2(Y,m,n) 在计算逆变换之前调整二维矩阵 Y 的大小。
  • 我们从一个简单的 3×3 矩阵 A 开始。
  • 我们使用 fft2() 计算 A 的二维傅里叶变换，结果为 Y。
  • 然后，我们使用 ifft2(Y, m, n) 将 Y 的大小调整为 4×5 矩阵（通过用零填充），并计算逆傅里叶变换，结果为 X。
  • 显示原始矩阵和调整大小后的矩阵以进行比较。

执行后，我们得到以下输出：

Original Matrix:
   1   2   3
   4   5   6
   7   8   9
Adjusted-size Matrix:
 Columns 1 through 4:

   0.4500 +      0i   0.9653 - 0.2010i   0.8126 - 0.0635i   1.2124 - 0.2270i
   2.0853 - 0.2853i   2.6006 - 0.4863i   2.4479 - 0.3488i   2.8477 - 0.5123i
   1.8000 - 0.7794i   2.3153 - 0.9804i   2.1626 - 0.8429i   2.5624 - 1.0064i
   2.8647 + 1.0647i   3.3800 + 0.8637i   3.2273 + 1.0012i   3.6271 + 0.8377i

 Column 5:

   1.0597 + 0.4915i
   2.6950 + 0.2062i
   2.4097 - 0.2879i
   3.4744 + 1.5562i

示例 3：指定二维逆傅里叶变换的对称性

我们的代码如下：

% Create a 2D matrix with complex values
A = [1+2i, 3-1i, 5+4i; -2+1i, 6-3i, 8+7i; 9-2i, 4+5i, -1-6i];

% Compute the 2D Fourier Transform
Y = fft2(A);

% Compute the Inverse Fourier Transform with symmetric treatment
X = ifft2(Y, 'symmetric');

% Display the original and reconstructed matrices
disp('Original Matrix:');
disp(A);

disp('Reconstructed Matrix:');
disp(X);
  • 此示例演示如何使用 ifft2(___,symflag) 在计算逆变换之前指定输入矩阵 Y 的对称性。
  • 我们从一个包含复数值的 3×3 矩阵 A 开始。
  • 我们使用 fft2() 计算 A 的二维傅里叶变换，结果为 Y。
  • 通过使用 ifft2(Y, 'symmetric')，我们计算 Y 的逆傅里叶变换，并进行对称处理，假设 Y 是共轭对称的。
  • 显示原始矩阵和重建矩阵以进行比较。

执行后，我们得到的输出是：

Original Matrix:
   1.0000 + 2.0000i   3.0000 - 1.0000i   5.0000 + 4.0000i
  -2.0000 + 1.0000i   6.0000 - 3.0000i   8.0000 + 7.0000i
   9.0000 - 2.0000i   4.0000 + 5.0000i  -1.0000 - 6.0000i

Reconstructed Matrix:
   -0.3472    5.6943    8.2717
   -9.3131    7.9245    8.7698
   15.3509    1.6906   -5.0415
打印页面
上一页
下一页
广告