MATLAB - 绘制正弦波

---

---

在 MATLAB 中绘制正弦波可以帮助你将周期性信号可视化并研究其特性。正弦波是信号处理、通信系统和许多其他领域的基础。MATLAB 提供了简单而强大的函数来生成和可视化正弦波。

在 MATLAB 中，有多种函数可用于绘制正弦波，包括：

• plot() 函数
• fplot() 函数
• ezplot() 函数
• stem() 函数
• polarplot() 函数

使用 plot() 函数

MATLAB 中的 plot() 函数是创建二维数据图的基本工具。它允许你通过绘制点并将它们用线连接起来来可视化数据中的关系和模式。使用 plot()，你可以创建各种类型的图，包括线图、散点图等等，这使得它成为数据分析和可视化的多功能工具。

语法

plot(X, Y)

MATLAB 中使用 **plot(X,Y)** 创建二维图，其中 X 和 Y 是表示要绘制点的 x 和 y 坐标的向量。X 和 Y 中每一对对应的元素定义图上的一个点。plot() 函数用线连接这些点，从而创建线图。

示例 1：使用 plot() 绘制正弦波

代码如下：

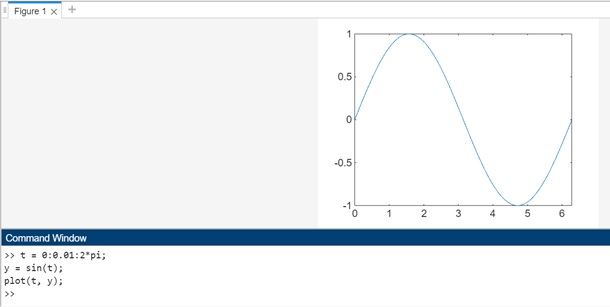
t = 0:0.01:2*pi; 
y = sin(t);
plot(t, y);

• 在这个例子中，我们首先使用冒号运算符 (:) 定义一个时间向量 t，生成从 0 到 2*pi 的值，步长为 0.01。
• 接下来，我们使用 sin() 函数计算与 t 中每个时间值对应的正弦值 y。
• 最后，我们使用 plot() 函数绘制正弦波，其中 t 为 x 值，y 为 y 值。这将创建一个以时间为 x 轴、幅度为 y 轴的正弦波图。

在 MATLAB 命令窗口中执行代码后，输出结果如下：

示例 2：绘制频率为 10 Hz 的正弦波

代码如下：

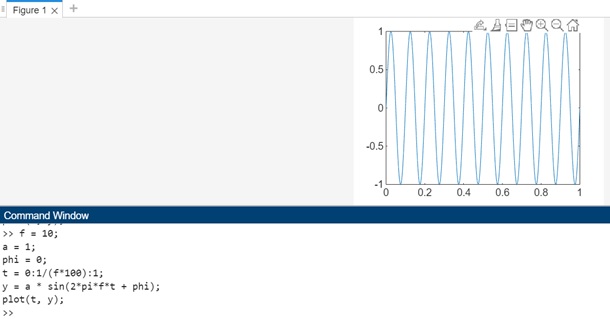
f = 10;     
a = 1;      
phi = 0;   
t = 0:1/(f*100):1;
y = a * sin(2*pi*f*t + phi);
plot(t, y);

在上例中：

• 代码定义了一个频率为 10 Hz (f = 10)，幅度为 1 伏特 (a = 1)，相位为 0 弧度 (phi = 0) 的正弦波。
• 它生成一个从 0 到 1 秒的时间向量 t，步长对应于频率，确保正弦波在一个指定的时间范围内完成一个周期。
• 正弦波方程 y = a * sin(2*pi*f*t + phi) 计算 t 中每个时间点的正弦波值，同时考虑频率、幅度、相位和时间向量。
• 最后，使用 plot() 函数绘制正弦波，并添加标签和标题以提高清晰度。

执行代码后，输出结果如下：

使用 fplot() 函数

MATLAB 中的 fplot() 函数用于在一个指定范围内绘制函数。它对于可视化数学函数（包括正弦波等三角函数）特别有用。与需要显式计算函数值的 plot() 函数不同，fplot() 可以直接绘制 y = f(x) 形式的函数。

语法

fplot(fun, [xmin, xmax])

fplot(fun, [xmin, xmax])：其中 fun：要绘制的函数。它可以是匿名函数或函数句柄。[xmin, xmax]：应绘制函数的 x 值范围。

示例：使用 fplot() 绘制正弦波

代码如下：

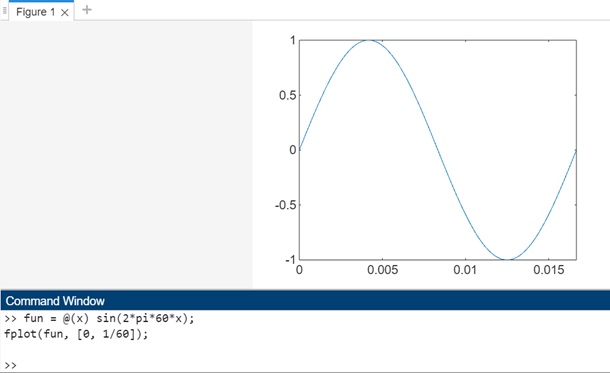
fun = @(x) sin(2*pi*60*x);
fplot(fun, [0, 1/60]);

在上例中

• 我们有一个表示频率为 60 Hz 的正弦波的匿名函数 fun。
• fplot() 函数用于在一个周期 (0 到 1/60 秒) 内绘制正弦波。
• x 轴表示时间（秒），y 轴表示正弦波的幅度。

执行代码后，输出结果如下：

使用 ezplot() 函数

MATLAB 中的 ezplot() 函数用于绘制二维隐式和显式方程。它对于可视化数学表达式特别有用，无需显式定义函数。ezplot() 可以处理单变量和参数表达式，使其成为各种绘图任务的多功能工具。

语法

ezplot(equation)
ezplot(equation, [xmin, xmax])

• **方程** - 要绘制的方程。它可以是显式方程 y = f(x) 或隐式方程 f(x, y) = 0。
• **[xmin, xmax]** - （可选）应绘制方程的 x 值范围。

示例：使用 ezplot() 绘制正弦波

代码如下：

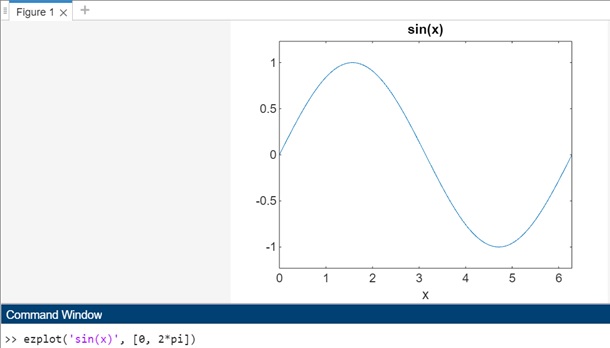
ezplot('sin(x)', [0, 2*pi])

上面的代码是：

• ezplot() 函数用于在 [0, 2*pi] 范围内绘制正弦波 y = sin(x)。
• 方程 'sin(x)' 表示正弦函数 sin(x)，其中 x 是自变量。
• 范围 [0, 2*pi] 指定绘制正弦波的 x 轴限制，涵盖正弦函数的一个完整周期。

执行代码后，输出结果为：

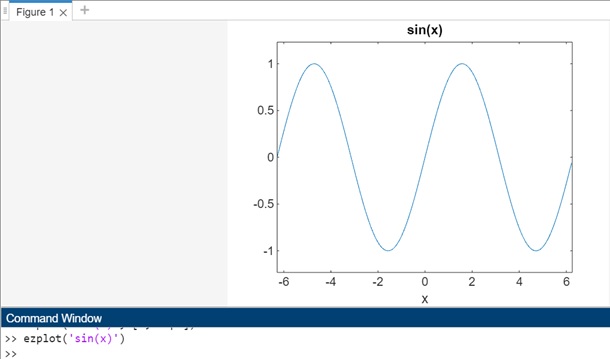
仅使用 ezplot('sin(x)')，输出结果如下：

使用 stem() 函数

MATLAB 中的 stem() 函数用于创建茎图，它类似于传统图，但将数据表示为基线上的离散点。茎图通常用于可视化离散数据，例如时间序列数据或信号样本。

语法

stem(Y)
stem(X, Y)

**Y** - 要绘制的数据值的向量。

**X** - 与 Y 中的数据值对应的 x 坐标的可选向量。

示例：正弦波的简单茎图

代码如下：

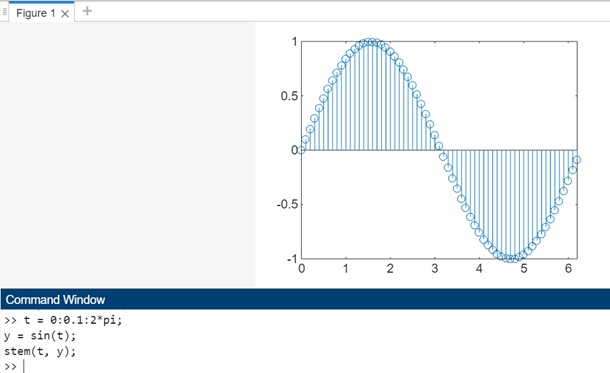
t = 0:0.1:2*pi;
y = sin(t);
stem(t, y);

在这个例子中，我们创建一个时间向量 t 并计算正弦值 y。

• stem() 函数用于绘制正弦波，其中 t 为 x 坐标，y 为 y 坐标。
• 该图将正弦波的离散样本表示为从 x 轴每个时间点上升的茎。

代码执行后的输出如下：

使用 polarplot() 函数

MATLAB 中的 polarplot() 函数用于创建极坐标图，这是一种使用极坐标而不是笛卡尔坐标的图表。极坐标图尤其适用于可视化周期性函数（例如正弦波）或以极坐标形式自然表示的数据。

语法

polarplot(theta, rho)

• theta − 每个数据点的角度向量（以弧度为单位）。
• rho − 每个数据点到原点的径向距离向量。

示例：使用 polarplot() 绘制正弦波

代码如下：

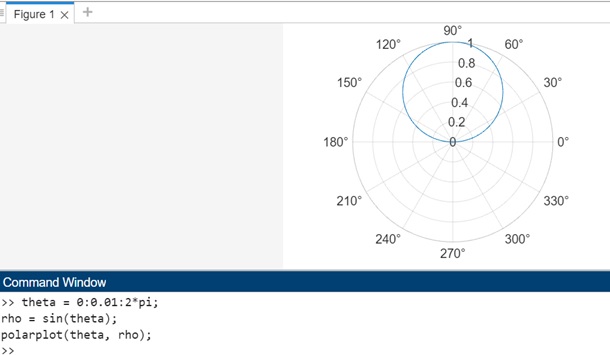
theta = 0:0.01:2*pi;
rho = sin(theta);
polarplot(theta, rho);

在这个例子中：

• 我们定义一个角度向量 theta，其范围从 0 到 2*pi（完整旋转一圈），步长很小。
• 我们将径向距离 rho 计算为与 theta 中每个角度对应的正弦值。
• polarplot() 函数用于在极坐标中绘制正弦波，其中 theta 为角度，rho 为径向距离。
• 生成的图将正弦波显示为围绕原点的螺旋线，其中到原点的距离表示每个角度下正弦波的幅度。

执行代码后，输出结果如下：