Network Theory

网络理论教程

网络理论教程

网络理论，也称为电路理论，是电气和电子工程学科的基本学科之一。网络理论提供了电量的基本定义、定律和分析电路的方法。您可以使用本教程作为指南来学习网络理论或电路理论的原理。

本教程涵盖了诸如电荷、电流、电压、电动势、欧姆定律、基尔霍夫定律、诺顿定理、戴维南定理、节点和网孔分析、交流电路、三相电路、电力、二端口网络等主题。

Network Theory Tutorial

电路理论知识对于设计、分析和排除各种电路和系统的故障至关重要。本教程提供了电路的理论和实践知识。对于希望了解学习电气和电子工程所需的基本概念的学生来说，本教程可以被认为是非常有用的资源。

电路理论导论

电路理论是电气和电子工程中最基本的学科，它涉及电气电路和网络的设计、分析和研究。它也被称为网络理论、网络分析、电路分析、电路基础等。

电路理论提供了合成和分析各种应用（如电机、电力电子、电力系统、通信系统、信号处理等）的电气电路所需的定律、原理和方法。

什么是电气网络？

在电气工程中，网络只不过是电气元件（如电阻、电感、电容、导线、电池等）的互连布置。

如果一个电气网络具有能量源并且有一个电流流动的闭合路径，则称为电路。

下图描绘了一个典型的电气网络和一个电路：

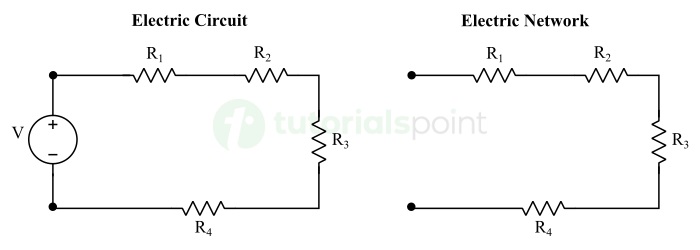
What is a Network in Electrical?

什么是网络分析？

网络分析或电路分析是确定电路中电激发或响应的过程。

换句话说，网络分析是确定电路中各个元件上的电压和流过它们的电流的过程。

在电路理论中，有几种可用于分析电路的定律和方法，例如欧姆定律、KCL、KVL、戴维南定理、诺顿定理、叠加定理等。

网络理论中的重要定义

以下是一些在网络理论中起着至关重要作用的关键定义：

电路元件

具有两个或多个端子的电气设备，并允许电流流过，称为电路元件。它也称为电路元素。

节点

在电路中，两个或多个元件连接在一起的点称为节点。具有接地电位的节点被认为是电路中的参考节点，它用于电路分析的目的。

结点

电路中三个或多个元件连接在一起的节点称为结点。

支路

电路中两个结点之间的部分称为支路。

回路和网孔

电气元件的闭合路径称为回路。网孔是一个基本回路，它不包含任何其他回路。

端口

电路的输入和输出端子称为端口。例如，电池的两个端子是其输出端口。

传递函数

传递函数是一个数学表达式，表示电路的输入和输出之间的关系。

元件传递函数

对于只有两个端子（即单端口元件）的电路，传递函数以阻抗或导纳为单位计算，称为元件传递函数。

等效电路

复杂电路或网络的简化版本，具有相同的输入和输出，称为等效电路。如果两个电路在同一对端子之间具有相同的电压和电流关系，则称这两个电路彼此等效。

电阻电路

仅具有电阻作为能量消耗元件和电流或电压源作为能量供应元件的电路称为电阻电路。

为什么电路理论很重要？

电路理论是电气和电子工程领域的重要学科，原因如下：

  • 它提供了轻松分析电路的定律、原理和方法。
  • 它允许工程师设计和合成我们日常生活中使用的设备和系统的电路。
  • 它还提供了电路分析工具，使它们更加可靠和高效。
  • 它为理解电力系统、电力电子、模拟电子、电机和驱动等电气工程中的复杂概念奠定了基础。
  • 它提供了故障排除和优化电气系统的工具。

电路理论的优缺点

电路理论提供了一个处理各种电路和系统的科学框架。但是，它既有优点也有局限性，在下表中突出显示：

电路理论的优点 电路理论的缺点
电路理论提供了关于电路定律、定理和原理的全面知识。 电路理论主要假设电路元件（如R、L、C等）是集总的和线性的。在处理分布式和非线性元件时，它有一些局限性。
电路理论提供了各种有效的方法将复杂电路简化为更简单的版本。 对于非线性电路，电路分析理论变得更加复杂，需要其他方法。
电路理论具有广泛的应用，从基础物理学到现代电力系统和机器人技术。 在电磁场占主导地位的地方（如天线设计）电路理论变得无效。
电路理论提供了交流 (AC) 和直流 (DC) 电路的分析技术。 电路理论中的许多概念都是基于理想假设，并在实际应用中引入了缺陷。
电路理论还提供了一些工具和技术来设计和合成高效的电路和系统。 电路理论有时无法模拟某些特定类型的功率损耗和噪声，如介质损耗、辐射损耗等。

电路理论的应用

电路理论是整个电气和电子工程的支柱，它具有广泛的应用。下面列出了电路理论在各个领域的某些主要应用：

  • 电力系统 - 电力系统中的电路理论有助于设计和实施可靠高效的电力传输和分配电网。
  • 电子学 - 电路理论在模拟和数字电子学中发挥着至关重要的作用，因为它允许设计高效的电子电路，如放大器、整流器、削波器、滤波器、振荡器等。
  • 信号与系统 - 电路理论也可用于信号与系统中分析和处理信号。
  • 消费电子产品 - 电路理论用于设计计算机、笔记本电脑、手机、电视等电子设备的电路。它也用于分析和排除这些设备的故障。
  • 通信系统 - 电路理论有助于开发通信系统中使用的放大器、发射机、接收机、滤波器等电路。

这些电路理论应用示例证明了它在电气和电子工程领域的通用性。

您将在网络理论教程中学习什么？

本网络理论综合教程涵盖了大量重要主题，这些主题是发展电路基础和掌握电气和电子工程中其他高级概念所必需的。下表给出了本教程中涵盖的每个章节的基本概述：

章节 描述
网络理论概述 本章介绍了网络理论中的基本概念，如电路和网络的概念、基本电量、电路元件的类型等。
网络理论中的有源元件 在本章中，您将了解什么是电路中的有源元件？您还将学习独立源和受控源。
网络理论中的无源元件 在本节中，我们将详细讨论电路中的三个关键无源元件，即电阻、电感和电容。
基尔霍夫定律 本章解释了网络理论中两个最基本的定律，即KCL（基尔霍夫电流定律）和KVL（基尔霍夫电压定律）。
电量分配原理 在本节中，您将学习电路的两个原理，即电压分配规则和电流分配规则。
节点分析 本节详细解释了如何使用节点分析方法求解电路。
网孔分析 在本章中，您将了解使用网孔分析方法求解电路的过程和应用。
等效电路 本章演示了将复杂的串联和并联电路简化到其最简单形式的方法。
三角形到星形转换 本章解释了将三角形网络表示为其等效星形网络的过程。
星形到三角形转换 本节演示了将星形网络转换为其等效三角形网络的过程。
网络拓扑 在本章中，您将学习网络拓扑（图论）的概念、图论的基本术语以及不同类型的网络图。
网络拓扑矩阵 本章讨论了网络拓扑矩阵，这些矩阵可用于通过使用其等效图来解决任何电路或网络问题。
叠加定理 在本章中，您将找到关于使用叠加定理求解电路的详细解释。
戴维南定理 本章提供了关于戴维南定理求解电路的分步说明。
诺顿定理 本章通过求解示例解释了使用诺顿定理求解电路的方法。
最大功率传输定理 本章描述了最大功率传输定理的陈述，以及最大功率传输的条件和最大功率传输时的效率。
直流电路响应 在本章中，您将了解直流电路的暂态和稳态响应，并将学习如何找到串联RL电路的响应。
交流电路响应 本章描述了求解串联RL电路交流响应的过程。
串联谐振 本章定义了谐振，并提供了对串联谐振电路的研究。
并联谐振 在本章中，您将学习并联谐振电路中的电路图和电气量。
耦合电路 本节概述了耦合电路和电路中耦合的类型。
二端口网络 本章描述了二端口网络和不同类型的二端口网络参数。
二端口参数转换 在本章中，您将学习转换二端口网络参数的过程。
滤波器 本节描述了电路中不同类型的滤波器。

网络理论常见问题解答

在本节中，我们收集了一些关于网络理论的常见问题解答 (FAQ)，以及它们的答案。

在电气工程中，网络理论是一门核心学科，它使用数学原理研究电路，以确定其行为。它有助于分析包含电阻、电容、电感和电源的电路。
叠加定理是用于分析包含多个独立电源的电路的基本定理。在此定理中，分别确定电路对每个独立电源的响应，并通过将每个电源的响应相加来确定电路的最终响应。
基尔霍夫提出了两个用于电路分析的基本定律，称为基尔霍夫电流定律 (KCL) 和基尔霍夫电压定律 (KVL)。KCL 提供了一种计算电路中节点进入和离开的总电流的方法，而 KVL 说明了在闭合路径周围查找总电压的方法。
节点分析和网孔分析的主要区别在于，节点分析基于KCL（基尔霍夫电流定律），而网孔分析基于KVL（基尔霍夫电压定律）。
戴维南定理和诺顿定理都可将复杂的线性电网络简化为最简单的形式以进行分析。其中，戴维南定理将复杂电路简化为一个等效的简化电路，该电路包含一个电压源和一个与之串联的电阻。另一方面，诺顿定理将复杂电路简化为一个等效的简化电路，该电路包含一个电流源和一个与之并联的电阻。

在串联电路中，如果连接了N个电阻，则串联电路的总电阻使用以下关系式计算：

$$\mathrm{R_t = R_1 + R_2 + R_3 + \dots + R_N}$$

类似地，在由N个电阻组成的并联电路中，总电阻使用以下表达式计算：

$$\mathrm{\frac{1}{R_t} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots + \frac{1}{R_N}}$$

并联电路中有一种特殊情况，当只有两个电阻并联连接时，总电阻计算如下：

$$\mathrm{R_t = \frac{R_1 R_2}{R_1 + R_2}}$$

在RLC电路中，谐振是在特定频率（称为谐振频率）下发生的一种状态，在此频率下，感抗与容抗大小相等且方向相反，从而相互抵消。在谐振条件下，RLC电路表现为纯电阻电路。
拉普拉斯变换 (LT) 是一种数学技术，用于在电路分析中将时域微分方程转换为s域中的简单代数方程。它主要用于分析包含电容器和电感的电路的暂态行为。

电容器和电感器在交流和直流电路中的行为如下：

  • 在直流电路中，电容器在充电后阻断直流电流，而电感器允许直流电流通过。
  • 在交流电路中，电容器允许交流电流通过，而电感器试图阻断交流电流的变化。

有时在处理电路时，我们会发现一些连接既不是串联也不是并联。相反，它们以三角形 (Δ) 或星形 (Y) 配置连接。

为了简化包含三角形 (Δ) 和星形 (Y) 连接的电路的分析，我们需要将三角形转换为星形或星形转换为三角形。这些方法被称为三角形-星形变换和星形-三角形变换。

打印页面
上一页
下一页
广告