网络理论 - 二端口网络

---

---

一般来说，如果用等效模型表示任何电路网络，则很容易分析该网络，该模型给出了输入和输出变量之间的关系。为此，我们可以使用二端口网络表示。顾名思义，二端口网络包含两个端口。其中一个端口用作输入端口，另一个端口用作输出端口。第一个和第二个端口分别称为端口1和端口2。

单端口网络是一个双端电路网络，其中电流从一个端子进入，从另一个端子离开。电阻器、电感器和电容器是单端口网络的例子，因为每个网络都有两个端子。单端口网络表示如下图所示。

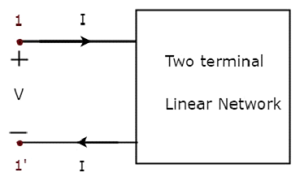
这里，端子对1和1'代表一个端口。在这种情况下，我们只有一个端口，因为它是一个单端口网络。

类似地，二端口网络是一对双端电路网络，其中电流从每个端口的一个端子进入，从另一个端子离开。二端口网络表示如下图所示。

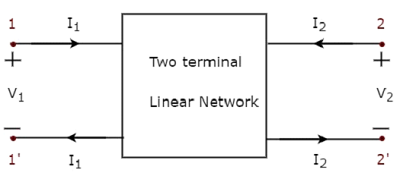
这里，一对端子1和1'代表一个端口，称为端口1；另一对端子2和2'代表另一个端口，称为端口2。

如图所示，二端口网络中有四个变量V₁、V₂、I₁和I₂。其中，我们可以选择两个变量作为自变量，另外两个变量作为因变量。因此，我们将得到六对可能的方程。这些方程用自变量表示因变量。自变量的系数称为参数。因此，每一对方程将给出一组四个参数。

二端口网络参数

二端口网络的参数称为二端口网络参数，或简称为二端口参数。以下是二端口网络参数的类型。

• Z参数
• Y参数
• T参数
• T'参数
• h参数
• g参数

现在，让我们逐一讨论这些二端口网络参数。

Z参数

通过将变量V₁和V₂视为因变量，将I₁和I₂视为自变量，我们将得到以下两对方程。自变量I₁和I₂的系数称为Z参数。

$$V_1 = Z_{11} I_1 + Z_{12} I_2$$

$$V_2 = Z_{21} I_1 + Z_{22} I_2$$

Z参数为

$$Z_{11} = \frac{V_1}{I_1}, \: 当 \: I_2 = 0$$

$$Z_{12} = \frac{V_1}{I_2}, \: 当 \: I_1 = 0$$

$$Z_{21} = \frac{V_2}{I_1}, \: 当 \: I_2 = 0$$

$$Z_{22} = \frac{V_2}{I_2}, \: 当 \: I_1 = 0$$

Z参数称为阻抗参数，因为它们只是电压和电流的比值。Z参数的单位是欧姆(Ω)。

我们可以通过对端口2进行开路来计算两个Z参数Z₁₁和Z₂₁。类似地，我们可以通过对端口1进行开路来计算另外两个Z参数Z₁₂和Z₂₂。因此，Z参数也称为开路阻抗参数。

Y参数

通过将变量I₁和I₂视为因变量，将V₁和V₂视为自变量，我们将得到以下两对方程。自变量V₁和V₂的系数称为Y参数。

$$I_1 = Y_{11} V_1 + Y_{12} V_2$$

$$I_2 = Y_{21} V_1 + Y_{22} V_2$$

Y参数为

$$Y_{11} = \frac{I_1}{V_1}, \: 当 \: V_2 = 0$$

$$Y_{12} = \frac{I_1}{V_2}, \: 当 \: V_1 = 0$$

$$Y_{21} = \frac{I_2}{V_1}, \: 当 \: V_2 = 0$$

$$Y_{22} = \frac{I_2}{V_2}, \: 当 \: V_1 = 0$$

Y参数称为导纳参数，因为它们只是电流和电压的比值。Y参数的单位是姆欧。

我们可以通过对端口2进行短路来计算两个Y参数Y₁₁和Y₂₁。类似地，我们可以通过对端口1进行短路来计算另外两个Y参数Y₁₂和Y₂₂。因此，Y参数也称为短路导纳参数。

T参数

通过将变量V₁和I₁视为因变量，将V₂和I₂视为自变量，我们将得到以下两对方程。V₂和-I₂的系数称为T参数。

$$V_1 = A V_2 - B I_2$$

$$I_1 = C V_2 - D I_2$$

T参数为

$$A = \frac{V_1}{V_2}, \: 当 \: I_2 = 0$$

$$B = -\frac{V_1}{I_2}, \: 当 \: V_2 = 0$$

$$C = \frac{I_1}{V_2}, \: 当 \: I_2 = 0$$

$$D = -\frac{I_1}{I_2}, \: 当 \: V_2 = 0$$

T参数称为传输参数或ABCD参数。参数A和D没有单位，因为它们是无量纲的。参数B和C的单位分别是欧姆和姆欧。

我们可以通过对端口2进行开路来计算两个参数A和C。类似地，我们可以通过对端口2进行短路来计算另外两个参数B和D。

T'参数

通过将变量V₂和I₂视为因变量，将V₁和I₁视为自变量，我们将得到以下两对方程。V₁和-I₁的系数称为T'参数。

$$V_2 = A' V_1 - B' I_1$$

$$I_2 = C' V_1 - D' I_1$$

T'参数为

$$A' = \frac{V_2}{V_1}, \: 当\: I_1 = 0$$

$$B' = -\frac{V_2}{I_1}, \: 当\: V_1 = 0$$

$$C' = \frac{I_2}{V_1}, \: 当\: I_1 = 0$$

$$D' = -\frac{I_2}{I_1}, \: 当 \: V_1 = 0$$

T'参数称为反向传输参数或A'B'C'D'参数。参数A'和D'没有单位，因为它们是无量纲的。参数B'和C'的单位分别是欧姆和姆欧。

我们可以通过对端口1进行开路来计算两个参数A'和C'。类似地，我们可以通过对端口1进行短路来计算另外两个参数B'和D'。

h参数

通过将变量V₁和I₂视为因变量，将I₁和V₂视为自变量，我们将得到以下两对方程。自变量I₁和V₂的系数称为h参数。

$$V_1 = h_{11} I_1 + h_{12} V_2$$

$$I_2 = h_{21} I_1 + h_{22} V_2$$

h参数为

$$h_{11} = \frac{V_1}{I_1},\: 当\: V_2 = 0$$

$$h_{12} = \frac{V_1}{V_2},\: 当\: I_1 = 0$$

$$h_{21} = \frac{I_2}{I_1},\: 当\: V_2 = 0$$

$$h_{22} = \frac{I_2}{V_2},\: 当\: I_1 = 0$$

h参数称为混合参数。参数h₁₂和h₂₁没有单位，因为它们是无量纲的。参数h₁₁和h₂₂的单位分别是欧姆和姆欧。

我们可以通过对端口2进行短路来计算两个参数h₁₁和h₂₁。类似地，我们可以通过对端口1进行开路来计算另外两个参数h₁₂和h₂₂。

h参数或混合参数在晶体管建模电路（网络）中很有用。

g参数

通过将变量I₁和V₂视为因变量，将V₁和I₂视为自变量，我们将得到以下两对方程。自变量V₁和I₂的系数称为g参数。

$$I_1 = g_{11} V_1 + g_{12} I_2$$

$$V_2 = g_{21} V_1 + g_{22} I_2$$

g参数为

$$g_{11} = \frac{I_1}{V_1},\: 当\: I_2 = 0$$

$$g_{12} = \frac{I_1}{I_2},\: 当\: V_1 = 0$$

$$g_{21} = \frac{V_2}{V_1},\: 当\: I_2 = 0$$

$$g_{22} = \frac{V_2}{I_2},\: 当 \: V_1 = 0$$

g参数称为反向混合参数。参数g₁₂和g₂₁没有单位，因为它们是无量纲的。参数g₁₁和g₂₂的单位分别是姆欧和欧姆。

我们可以通过对端口2进行开路来计算两个参数g₁₁和g₂₁。类似地，我们可以通过对端口1进行短路来计算另外两个参数g₁₂和g₂₂。