网络理论 - 基尔霍夫定律

---

---

网络元件可以是有源或无源类型。任何电路或网络都包含这两种类型的网络元件之一或两者结合。

现在，让我们讨论以下两个定律，它们通常被称为基尔霍夫定律。

• 基尔霍夫电流定律
• 基尔霍夫电压定律

基尔霍夫电流定律

基尔霍夫电流定律 (KCL) 指出，离开（或进入）节点的所有电流的代数和等于零。

节点是指两个或多个电路元件连接在一起的点。如果只有两个电路元件连接到一个节点，则称为简单节点。如果三个或更多电路元件连接到一个节点，则称为主节点。

数学上，KCL 可以表示为

$$\displaystyle\sum\limits_{m=1}^M I_m = 0$$

其中，

• I_m 是离开节点的第 m 个支路电流。

• M 是连接到节点的支路数量。

上述KCL的陈述也可以表示为“进入节点的所有电流的代数和等于离开节点的所有电流的代数和”。让我们通过以下示例来验证此陈述。

示例

在以下图形的节点P处写出KCL 方程。

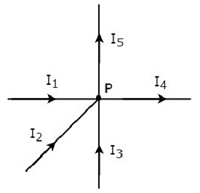
• 在上图中，支路电流 I₁、I₂ 和 I₃ 进入节点 P。因此，对这三个电流考虑负号。

• 在上图中，支路电流 I₄ 和 I₅ 离开节点 P。因此，对这两个电流考虑正号。

节点 P 处的KCL 方程将是

$$- I_1 - I_2 - I_3 + I_4 + I_5 = 0$$

$$\Rightarrow I_1 + I_2 + I_3 = I_4 + I_5$$

在上式中，左侧表示进入电流的总和，而右侧表示离开电流的总和。

在本教程中，当电流离开节点时，我们将考虑正号，而当电流进入节点时，我们将考虑负号。同样，您可以考虑当电流离开节点时使用负号，而当电流进入节点时使用正号。在这两种情况下，结果都相同。

注意 - KCL 与连接到节点的网络元件的性质无关。

基尔霍夫电压定律

基尔霍夫电压定律 (KVL) 指出，围绕回路或网孔的所有电压的代数和等于零。

回路是指从同一个节点开始并终止于同一个节点的路径。相比之下，网孔是指不包含任何其他回路的回路。

数学上，KVL 可以表示为

$$\displaystyle\sum\limits_{n=1}^N V_n = 0$$

其中，

• V_n 是回路（网孔）中第 n 个元件的电压。

• N 是回路（网孔）中网络元件的数量。

上述KVL的陈述也可以表示为“电压源的代数和等于回路中存在的电压降的代数和”。让我们借助以下示例来验证此陈述。

示例

在以下电路的回路周围写出KVL 方程。

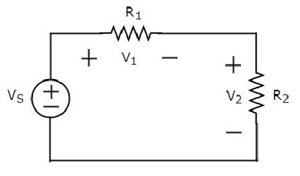
上述电路图由一个电压源 V_S 与两个电阻 R₁ 和 R₂ 串联组成。电阻 R₁ 和 R₂ 上的电压降分别为 V₁ 和 V₂。

围绕回路应用KVL。

$$V_S - V_1 - V_2 = 0$$

$$\Rightarrow V_S = V_1 + V_2$$

在上式中，左侧项表示单个电压源 VS。而右侧表示电压降的总和。在这个例子中，我们只考虑了一个电压源。因此，左侧只包含一项。如果我们考虑多个电压源，则左侧包含电压源的总和。

在本教程中，我们考虑每个元件电压的符号作为围绕回路行进时存在的第二个端子的极性。同样，您可以考虑每个电压的符号作为围绕回路行进时存在的第一个端子的极性。在这两种情况下，结果都相同。

注意 - KVL 与回路中存在的网络元件的性质无关。