等效电路例题

在上一章中，我们讨论了串联组合和并联组合的等效电路。本章我们通过考虑相似无源元件的串联和并联组合来解决一个例题。

例题

让我们求解以下电路网络中A&B两端之间的等效电阻。

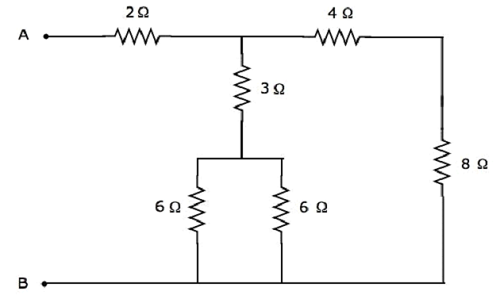
我们将通过将上述网络简化为这两端之间的一个单一电阻来得到A&B两端之间的等效电阻。为此，我们必须识别以串联和并联形式连接的电阻组合，然后在每一步中找到各自形式的等效电阻。

给定的电路网络被修改成如下所示的形式。

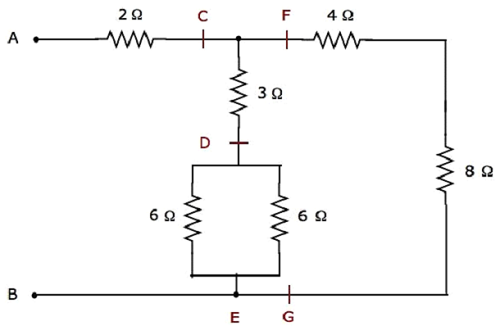
在上图中，字母C到G用于标记各个节点。

步骤1 - 在上述网络中，两个6 Ω电阻并联连接。因此，D&E之间的等效电阻将为3 Ω。这可以通过以下简化得到。

$$R_{DE} = \frac{6 \times 6}{6 + 6} = \frac{36}{12} = 3 \Omega$$

在上图网络中，4 Ω和8 Ω的电阻串联连接。因此，F&G之间的等效电阻将为12 Ω。这可以通过以下简化得到。

$$R_{FG} = 4 + 8 = 12 \Omega$$

步骤2 - 步骤1之后简化的电路网络如下图所示。

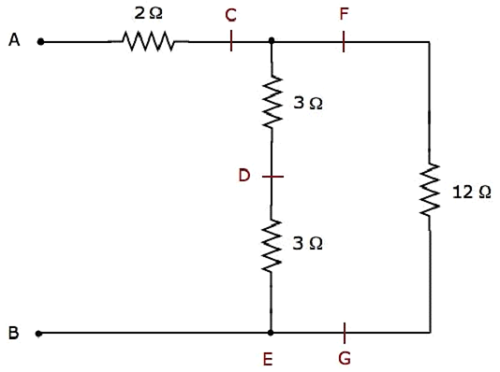
在上图网络中，两个3 Ω电阻串联连接。因此，C&E之间的等效电阻将为6 Ω。这可以通过以下简化得到。

$$R_{CE} = 3 + 3 = 6 \Omega$$

步骤3 - 步骤2之后简化的电路网络如下图所示。

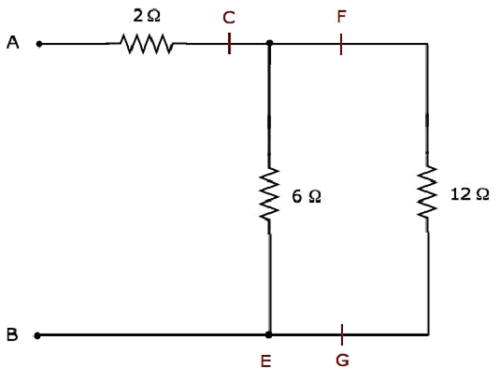
在上图网络中，6 Ω和12 Ω的电阻并联连接。因此，C&B之间的等效电阻将为4 Ω。这可以通过以下简化得到。

$$R_{CB} = \frac{6 \times 12}{6 + 12} = \frac{72}{18} = 4 \Omega$$

步骤4 - 步骤3之后简化的电路网络如下图所示。

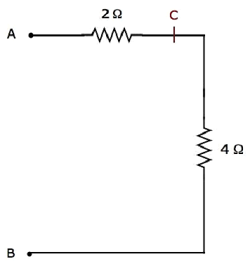
在上图网络中，2 Ω和4 Ω的电阻在A&B端之间串联连接。因此，A&B之间的等效电阻将为6 Ω。这可以通过以下简化得到。

$$R_{AB} = 2 + 4 = 6 \Omega$$

因此，给定电路网络中A&B两端之间的等效电阻为6 Ω。