网络理论 - 诺顿定理

---

---

诺顿定理类似于戴维南定理。它指出，任何一个双端线性网络或电路都可以用一个等效的网络或电路来表示，该网络或电路由一个与电阻并联的电流源组成。它被称为诺顿等效电路。线性电路可能包含独立源、相关源和电阻。

如果一个电路有多个独立源、相关源和电阻，那么某个元件上的响应可以通过将该元件左侧的整个网络替换为诺顿等效电路来轻松找到。

元件上的响应可以是该元件上的电压、流过该元件的电流或该元件上消耗的功率。

此概念在下面的图中进行了说明。

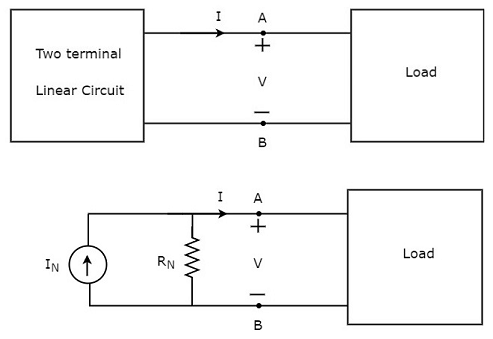
诺顿等效电路类似于一个实际的电流源。因此，它有一个与电阻并联的电流源。

• 诺顿等效电路中存在的电流源称为诺顿等效电流或简称为诺顿电流 I_N。

• 诺顿等效电路中存在的电阻称为诺顿等效电阻或简称为诺顿电阻 R_N。

求诺顿等效电路的方法

有三种方法可以求诺顿等效电路。根据网络中存在的源类型，我们可以选择这三种方法之一。现在，让我们逐一讨论这三种方法。

方法 1

当只有独立类型的电源存在时，请按照以下步骤找到诺顿等效电路。

• 步骤 1 - 通过打开要查找诺顿等效电路的端子来考虑电路图。

• 步骤 2 - 通过短接上述电路的两个打开的端子来找到诺顿电流I_N。

• 步骤 3 - 通过消除步骤 1 中考虑的电路中存在的独立源，找到电路的打开端子上的诺顿电阻R_N。诺顿电阻R_N将与戴维南电阻R_Th相同。

• 步骤 4 - 通过将诺顿电流 IN 与诺顿电阻 R_N 并联连接来绘制诺顿等效电路。

现在，我们可以找到位于诺顿等效电路右侧的元件的响应。

方法 2

当独立类型和相关类型的电源都存在时，请按照以下步骤找到诺顿等效电路。

• 步骤 1 - 通过打开要查找诺顿等效电路的端子来考虑电路图。

• 步骤 2 - 找到上述电路的开路端子上的开路电压V_OC。

• 步骤 3 - 通过短接上述电路的两个打开的端子来找到诺顿电流I_N。

• 步骤 4 - 使用以下公式找到诺顿电阻R_N。

$$R_N = \frac{V_{OC}}{I_N}$$

• 步骤 5 - 通过将诺顿电流 I_N 与诺顿电阻 R_N 并联连接来绘制诺顿等效电路。

现在，我们可以找到位于诺顿等效电路右侧的元件的响应。

方法 3

这是查找诺顿等效电路的另一种方法。

• 步骤 1 - 在所需的两个端子之间找到一个戴维南等效电路。我们知道它由一个戴维南电压源 V_Th 和一个戴维南电阻 R_Th 组成。

• 步骤 2 - 对上述戴维南等效电路应用电源变换技术。我们将得到诺顿等效电路。这里，

诺顿电流，

$$I_N = \frac{V_{Th}}{R_{Th}}$$

诺顿电阻，

$$R_N = R_{Th}$$

此概念在下面的图中进行了说明。

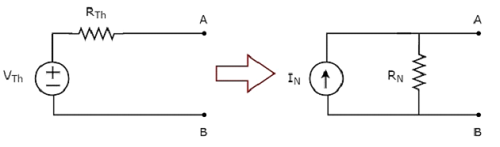
现在，我们可以通过将诺顿等效电路放置在该元件的左侧来找到元件的响应。

注意 - 同样，我们可以通过首先找到诺顿等效电路，然后对其应用电源变换技术来找到戴维南等效电路。此概念在下面的图中进行了说明。

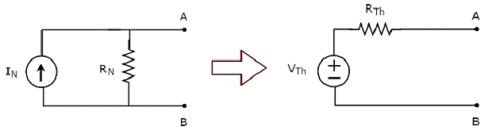
这是查找戴维南等效电路的方法 3。

示例

首先找到端子 A 和 B 左侧的诺顿等效电路，然后找到流过 20 Ω 电阻的电流。

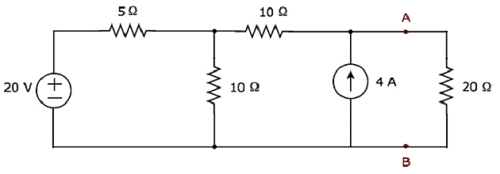
让我们使用方法 3解决此问题。

步骤 1 - 在上一章中，我们计算了端子 A 和 B 左侧的戴维南等效电路。我们现在可以使用此电路。它显示在下面的图中。

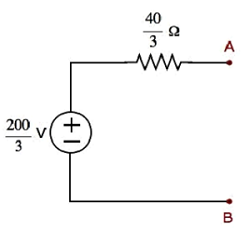
这里，戴维南电压，$V_{Th} = \frac{200}{3} V$ 和戴维南电阻，$R_{Th} = \frac{40}{3} \Omega$

步骤 2 - 对上述戴维南等效电路应用电源变换技术。将V_Th 和R_Th 的值代入以下诺顿电流公式。

$$I_N = \frac{V_{Th}}{R_{Th}}$$

$$I_N = \frac{\frac{200}{3}}{\frac{40}{3}} = 5A$$

因此，诺顿电流I_N 为5 A。

我们知道诺顿电阻R_N 与戴维南电阻R_Th 相同。

$$\mathbf {R_N = \frac{40}{3} \Omega}$$

与上述戴维南等效电路对应的诺顿等效电路显示在下面的图中。

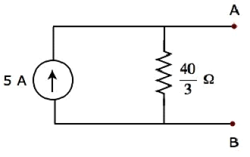
现在，将诺顿等效电路放置在给定电路的端子 A 和 B 的左侧。

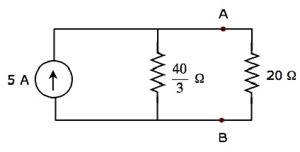
使用电流分配原理，流过 20 Ω 电阻的电流将为

$$I_{20 \Omega} = 5 \lgroup \frac{\frac{40}{3}}{\frac{40}{3} + 20} \rgroup$$

$$I_{20 \Omega} = 5 \lgroup \frac{40}{100} \rgroup = 2A$$

因此，流过 20 Ω 电阻的电流为2 A。