网络理论 - 网络拓扑

---

---

网络拓扑是电气电路的图形表示。它通过将复杂的电气电路转换为网络图来分析这些电路。网络拓扑也称为**图论**。

网络拓扑的基本术语

现在，让我们讨论一下网络拓扑中涉及的基本术语。

图

网络图简称为**图**。它由一组通过分支连接的节点组成。在图中，节点是两个或多个分支的公共点。有时，只有一个分支可能连接到节点。分支是连接两个节点的线段。

任何电气电路或网络都可以通过用短路代替无源元件和电压源，用开路代替电流源，将其转换为等效的**图**。这意味着图中的线段表示对应于电气电路的无源元件或电压源的分支。

示例

让我们考虑以下**电气电路**。

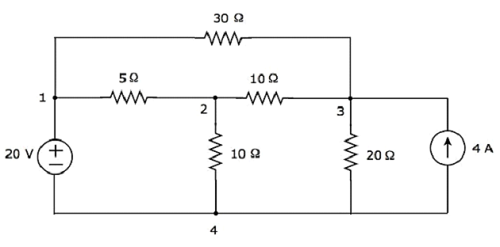
在上图中，有**四个主节点**，分别标记为 1、2、3 和 4。在上图中，有**七个分支**，其中一个分支包含一个 20 V 的电压源，另一个分支包含一个 4 A 的电流源，其余五个分支包含电阻，电阻值分别为 30 Ω、5 Ω、10 Ω、10 Ω 和 20 Ω。

与上述电气电路对应的等效**图**如下所示。

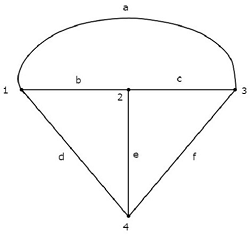
在上图中，有**四个节点**，分别标记为 1、2、3 和 4。它们与电气电路中的主节点相同。上图中有**六个分支**，分别标记为 a、b、c、d、e 和 f。

在这种情况下，我们在图中**少了一个分支**，因为在将电气电路转换为等效图时，4 A 的电流源被视为开路。

从这个例子中，我们可以得出以下结论 -

• 图中存在的**节点数**将等于电气电路中存在的主节点数。

• 图中存在的**分支数**将小于或等于电气电路中存在的分支数。

图的类型

以下是图的类型 -

• 连通图
• 非连通图
• 有向图
• 无向图

现在，让我们逐一讨论这些图。

连通图

如果图的任意两个节点之间至少存在一个分支，则称为**连通图**。这意味着连通图中的每个节点都将有一个或多个连接到它的分支。因此，没有节点会以孤立或分离的形式出现。

前面示例中显示的图是**连通图**。在这里，所有节点都由三个分支连接。

非连通图

如果图中至少存在一个节点，即使单个分支也没有连接到它，则称为**非连通图**。因此，非连通图中将存在一个或多个孤立节点。

考虑下图所示的图。

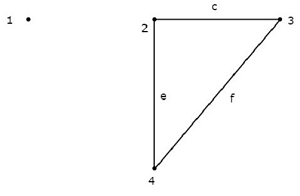
在此图中，节点 2、3 和 4 由两个分支连接。但是，甚至没有一个分支连接到**节点 1**。因此，节点 1 成为**孤立节点**。因此，上图是**非连通图**。

有向图

如果图的所有分支都用箭头表示，则该图称为**有向图**。这些箭头表示每个分支中电流流动的方向。因此，此图也称为**定向图**。

考虑下图所示的图。

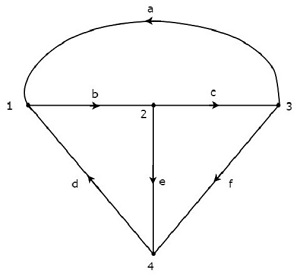
在上图中，每个分支中电流流动的方向都用箭头表示。因此，它是一个**有向图**。

无向图

如果图的分支没有用箭头表示，则该图称为**无向图**。由于没有电流流动的方向，因此此图也称为**无定向图**。

本章第一个示例中显示的图是**无定向图**，因为该图的分支上没有箭头。

子图及其类型

图的一部分称为**子图**。我们通过移除给定图的一些节点和/或分支来获得子图。因此，子图的分支和/或节点数将小于原始图。因此，我们可以得出结论，子图是图的子集。

以下是子图的**两种类型**。

• 树
• 余树

树

树是给定图的连通子图，它包含图的所有节点。但是，该子图中不应该有任何回路。树的分支称为**树枝**。

考虑以下本章开头示例中所示的图的**连通子图**。

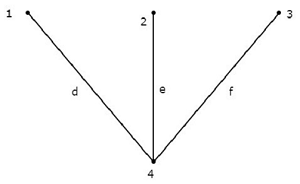
此连通子图包含给定图的所有四个节点，并且没有回路。因此，它是一棵**树**。

此树只有三个分支，而不是给定图的六个分支。因为，如果我们考虑给定图的其余分支中的任何一个分支，那么上述连通子图中将会有一个回路。然后，生成的连通子图将不是树。

从上面的树中，我们可以得出结论，树中存在的**分支数**应等于**n - 1**，其中“n”是给定图的节点数。

余树

余树是在形成树时移除的分支形成的子图。因此，它称为树的**补图**。对于每棵树，都将有一个相应的余树，其分支称为**连支**或弦。通常，连支用虚线表示。

与上述树对应的**余树**如下所示。

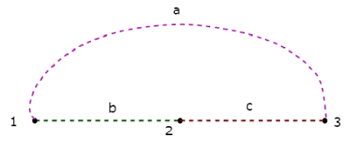
此余树只有三个节点，而不是给定图的四个节点，因为节点 4 与上述余树隔离。因此，余树不必是连通子图。此余树有三个分支，它们形成一个回路。

余树中存在的**分支数**将等于给定图的分支数与树枝数之差。在数学上，可以写成

$$l = b - (n - 1)$$

$$l = b - n + 1$$

其中，

• l 是连支数。
• b 是给定图中存在的分支数。
• n 是给定图中存在的节点数。

如果我们将树及其对应的余树组合起来，我们将得到如下所示的**原始图**。

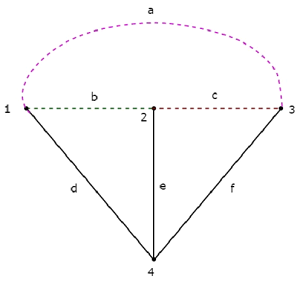
树枝 d、e 和 f 用实线表示。余树分支 a、b 和 c 用虚线表示。