网络理论 -交流电路的响应

---

---

在上一章中，我们讨论了直流电路的暂态响应和稳态响应。本章，让我们讨论一下交流电路的响应。我们在上一章中讨论的暂态响应和稳态响应的概念在这里也很有用。

求解RL串联电路的响应

考虑以下RL串联电路图。

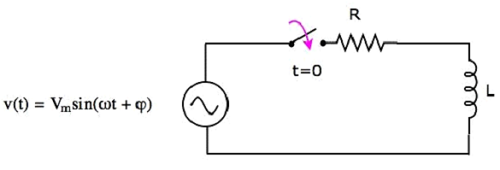
在上图电路中，开关一直处于t = 0之前的断开状态，并在t = 0时闭合。因此，在该时刻之前，具有V_m伏峰值电压的交流电压源未连接到RL串联电路。所以，电感器中没有初始电流。

当开关处于闭合位置时的电路图如下所示。

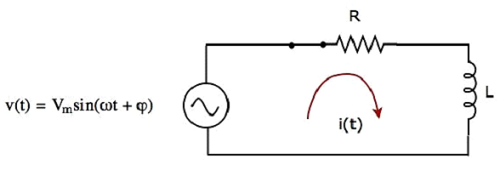
现在，由于具有V_m伏峰值电压的交流电压源已连接到RL串联电路，电流i(t)流过整个电路。

我们知道，流过上述电路的电流i(t)将包含两项，一项表示暂态部分，另一项表示稳态部分。

数学上，它可以表示为

$i(t) = i_{Tr}(t) + i_{ss}(t)$公式1

其中，

• $i_{Tr}(t)$是流过电路的电流的暂态响应。

• $i_{ss}(t)$是流过电路的电流的稳态响应。

在上一章中，我们得到了流过RL串联电路的电流的暂态响应。其形式为$Ke^{-\lgroup \frac{t}{\tau} \rgroup}$。

将$i_{Tr}(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup}$代入公式1。

$i(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup} + i_{ss}(t)$公式2

稳态电流的计算

如果将正弦信号作为输入施加到线性电路，则它会产生一个稳态输出，该输出也是一个正弦信号。输入和输出正弦信号将具有相同的频率，但幅度和相位角不同。

当正弦电压源激励线性电路时，我们可以使用拉普拉斯变换方法计算电路的稳态响应。

当开关处于闭合位置时的s域电路图如下所示。

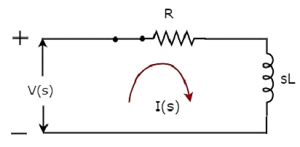
在上图电路中，所有量和参数都在s域表示。这些是时域量和参数的拉普拉斯变换。

上述电路的传递函数为

$$H(s) = \frac{I(s)}{V(s)}$$

$$\Rightarrow H(s) = \frac{1}{Z(s)}$$

$$\Rightarrow H(s) = \frac{1}{R + sL}$$

在上式中代入$s = j \omega$。

$$H(j \omega) = \frac{1}{R + j \omega L}$$

$\mathbf{\mathit{H(j \omega)}}$的幅值为

$$|H(j \omega)| = \frac{1}{\sqrt{R^2 + {\omega}^2 L^2}}$$

$\mathbf{\mathit{H(j \omega)}}$的相位角为

$$\angle H(j \omega) = -tan^{-1} \lgroup \frac{\omega L}{R} \rgroup$$

我们将通过以下两个步骤得到稳态电流$i_{ss}(t)$：

• 将输入正弦电压的峰值电压和$H(j \omega)$的幅值相乘。

• 将输入正弦电压和$H(j \omega)$的相位角相加。

稳态电流$i_{ss}(t)$将为

$$i_{ss}(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

将$i_{ss}(t)$的值代入公式2。

$i(t) = Ke^{-\lgroup \frac{t}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$公式3

我们知道电路中没有初始电流。因此，为了找到常数K的值，将t = 0和i(t) = 0代入公式3。

$$0 = Ke^{-\lgroup \frac{0}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega (0) + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

$$\Rightarrow 0 = K + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

$$\Rightarrow K = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

将K的值代入公式3。

$i(t) = - \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup e^{-\lgroup \frac{t}{\tau} \rgroup} + \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$公式4

公式4表示当RL串联电路由正弦电压源激励时流过它的电流。它包含两项。第一项和第二项分别表示电流的暂态响应和稳态响应。

我们可以忽略公式4的第一项，因为它的值远小于1。因此，流过电路的最终电流将为

$$i(t) = \frac{V_m}{\sqrt{R^2 +{\omega}^2 L^2}} sin \lgroup \omega t + \varphi - tan^{-1} \lgroup \frac {\omega L}{R}\rgroup \rgroup$$

它只包含稳态项。因此，我们只需要找到交流电路的稳态响应，而忽略其暂态响应。