网络理论 - 串联谐振

---

---

谐振是由于电路上存在电感和电容等储能元件而产生的。它是无线电和电视接收机设计的根本概念，它们的设计方式应能够仅选择所需的电台频率。

谐振主要分为两种类型，即串联谐振和并联谐振。这些分类是基于网络元件是串联还是并联连接。在本章中，让我们讨论串联谐振。

串联谐振电路图

如果谐振发生在串联 RLC 电路中，则称为串联谐振。考虑以下串联 RLC 电路，它以相量域表示。

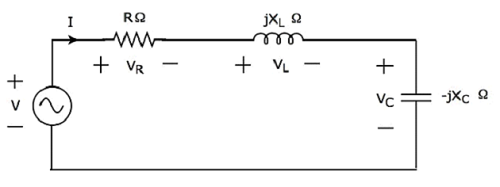
此处，电阻、电感和电容等无源元件串联连接。整个组合与输入正弦电压源串联。

对回路应用KVL。

$$V - V_R - V_L - V_C = 0$$

$$\Rightarrow V - IR - I(j X_L) - I(-j X_C) = 0$$

$$\Rightarrow V = IR + I(j X_L) + I(-j X_C)$$

$\Rightarrow V = I[R + j(X_L - X_C)]$公式 1

上述公式的形式为V = IZ。

因此，串联 RLC 电路的阻抗 Z 为

$$Z = R + j(X_L - X_C)$$

谐振时的参数和电量

现在，让我们逐一推导串联 RLC 电路谐振时参数和电量的值。

谐振频率

发生谐振的频率称为谐振频率 f_r。在串联 RLC 电路中，当阻抗 Z 的虚部为零时发生谐振，即 $X_L - X_C$ 的值应等于零。

$$\Rightarrow X_L = X_C$$

将 $X_L = 2 \pi f L$ 和 $X_C = \frac{1}{2 \pi f C}$ 代入上述公式。

$$2 \pi f L = \frac{1}{2 \pi f C}$$

$$\Rightarrow f^2 = \frac{1}{(2 \pi)^2 L C}$$

$$\Rightarrow f = \frac{1}{(2 \pi) \sqrt{LC}}$$

因此，串联 RLC 电路的谐振频率 f_r 为

$$f_r = \frac{1}{(2 \pi) \sqrt{LC}}$$

其中，L 是电感的电感值，C 是电容的电容值。

串联 RLC 电路的谐振频率 f_r 仅取决于电感L 和电容C。但它与电阻R 无关。

阻抗

我们得到串联 RLC 电路的阻抗 Z 为

$$Z = R + j(X_L - X_C)$$

将 $X_L = X_C$ 代入上述公式。

$$Z = R + j(X_C - X_C)$$

$$\Rightarrow Z = R + j(0)$$

$$\Rightarrow Z = R$$

在谐振时，串联 RLC 电路的阻抗 Z 等于电阻R 的值，即Z = R。

流过电路的电流

将 $X_L - X_C = 0$ 代入公式 1。

$$V = I[R + j(0)]$$

$$\Rightarrow V = IR$$

$$\Rightarrow I = \frac{V}{R}$$

因此，串联 RLC 电路在谐振时流过的电流为$\mathbf{\mathit{I = \frac{V}{R}}}$。

在谐振时，串联 RLC 电路的阻抗达到最小值。因此，在谐振时，最大电流流过该电路。

电阻两端的电压

电阻两端的电压为

$$V_R = IR$$

将I 的值代入上述公式。

$$V_R = \lgroup \frac{V}{R} \rgroup R$$

$$\Rightarrow V_R = V$$

因此，谐振时电阻两端的电压为V_R = V。

电感两端的电压

电感两端的电压为

$$V_L = I(jX_L)$$

将I 的值代入上述公式。

$$V_L = \lgroup \frac{V}{R} \rgroup (jX_L)$$

$$\Rightarrow V_L = j \lgroup \frac{X_L}{R} \rgroup V$$

$$\Rightarrow V_L = j QV$$

因此，谐振时电感两端的电压为$V_L = j QV$。

因此，谐振时电感两端的电压幅值为

$$|V_L| = QV$$

其中Q 为品质因数，其值为$\frac{X_L}{R}$

电容两端的电压

电容两端的电压为

$$V_C = I(-j X_C)$$

将I 的值代入上述公式。

$$V_C = \lgroup \frac{V}{R} \rgroup (-j X_C)$$

$$\Rightarrow V_C = -j \lgroup \frac{X_C}{R} \rgroup V$$

$$\Rightarrow V_C = -jQV$$

因此，谐振时电容两端的电压为$\mathbf{\mathit{V_C = -jQV}}$。

因此，谐振时电容两端的电压幅值为

$$|V_C| = QV$$

其中Q 为品质因数，其值为$\frac{X_{C}}{R}$

注意 - 串联谐振 RLC 电路称为电压放大电路，因为电感和电容两端的电压幅值等于输入正弦电压 V 的 Q 倍。