网络理论 - 星形到三角形转换

---

---

在上一章中，我们讨论了将三角形网络转换为等效星形网络。现在，让我们讨论如何将星形网络转换为等效三角形网络。这种转换称为星形到三角形转换。

在上一章中，我们得到了从三角形网络得到的星形网络电阻为

$R_A = \frac{R_1 R_2}{R_1 + R_2 + R_3}$ 公式1

$R_B = \frac{R_2 R_3}{R_1 + R_2 + R_3}$ 公式2

$R_C = \frac{R_3 R_1}{R_1 + R_2 + R_3}$ 公式3

根据星形网络电阻表示的三角形网络电阻

让我们对上述公式进行变换，以便根据星形网络的电阻得到三角形网络的电阻。

• 相乘每一组两个公式，然后相加。

$$R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2^2 R_3 + R_2 R_3^2 R_1 + R_3 R_1^2 R_2}{(R_1 + R_2 + R_3)^2}$$

$$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3(R_1 + R_2 + R_3)}{(R_1 + R_2 + R_3)^2}$$

$\Rightarrow R_A R_B + R_B R_C + R_C R_A = \frac{R_1 R_2 R_3}{R_1 + R_2 + R_3}$ 公式4

• 用公式2除以公式4，我们将得到

$$\frac{R_A R_B + R_B R_C + R_C R_A}{R_B} = R_1$$

$$\Rightarrow R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$

• 用公式3除以公式4，我们将得到

$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$

• 用公式1除以公式4，我们将得到

$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$

利用上述关系，我们可以根据星形网络的电阻找到三角形网络的电阻。通过这种方式，我们可以将星形网络转换为三角形网络。

示例

让我们计算三角形网络的电阻，它与下图所示的星形网络等效。

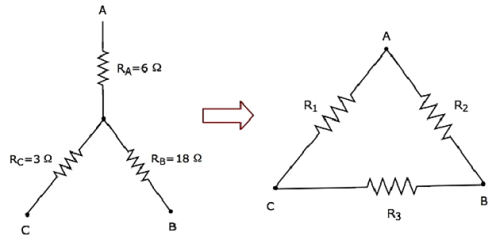
给定星形网络的电阻为R_A = 6 Ω, R_B = 18 Ω和R_C = 3 Ω。

我们知道根据星形网络电阻表示的三角形网络电阻的关系如下。

$$R_1 = R_C + R_A + \frac{R_C R_A}{R_B}$$

$$R_2 = R_A + R_B + \frac{R_A R_B}{R_C}$$

$$R_3 = R_B + R_C + \frac{R_B R_C}{R_A}$$

将R_A, R_B和R_C的值代入上述公式。

$$R_1 = 3 + 6 + \frac{3 \times 6}{18} = 9 + 1 = 10 \Omega$$

$$R_2 = 6 + 18 + \frac{6 \times 18}{3} = 24 + 36 = 60 \Omega$$

$$R_3 = 18 + 3 + \frac{18 \times 3}{6} = 21 + 9 = 30 \Omega$$

因此，我们得到了三角形网络的电阻为R₁ = 10 Ω, R₂ = 60 Ω和R₃ = 30 Ω，它们与给定星形网络的电阻等效。