机器学习中的偏差和方差

偏差和方差是机器学习中两个重要的概念，它们描述了模型预测中误差的来源。**偏差**指的是由于过度简化输入特征和输出变量之间底层关系而导致的误差。同时，**方差**指的是由于对训练数据中的波动过于敏感而导致的误差。

在机器学习中，我们努力**最小化偏差和方差**，以便构建一个能够准确预测未见数据的模型。高偏差模型可能过于简单，无法拟合训练数据。相反，方差高的模型可能会过拟合训练数据，无法推广到新数据。

通常，一个机器学习模型会显示三种类型的误差——偏差、方差和不可减少误差。偏差和方差误差之间存在权衡。减少偏差会导致方差增加，反之亦然。

什么是偏差？

偏差计算为平均预测值与实际值之间的差值。在机器学习中，偏差（系统误差）发生在模型对数据做出错误假设时。

高偏差模型既不匹配训练数据也不匹配测试数据。这会导致训练和测试数据中的误差很高。

而低偏差模型很好地匹配训练数据（高训练准确率或训练误差较小）。它导致训练数据中的误差较低，但测试数据中的误差较高。

偏差类型

• **高偏差** - 高偏差是由于机器学习模型中的错误假设造成的。高偏差模型无法捕捉训练数据中隐藏的模式。这会导致**欠拟合**。这会导致**欠拟合**。高偏差的特点是模型高度简化、欠拟合以及训练和测试数据中较高的误差。
• **低偏差** - 低偏差模型能够捕捉训练数据中隐藏的模式。低偏差会导致高方差，最终导致过拟合。低偏差通常是由于ML模型过于复杂造成的。

下图显示了高偏差和低偏差误差的图形表示。

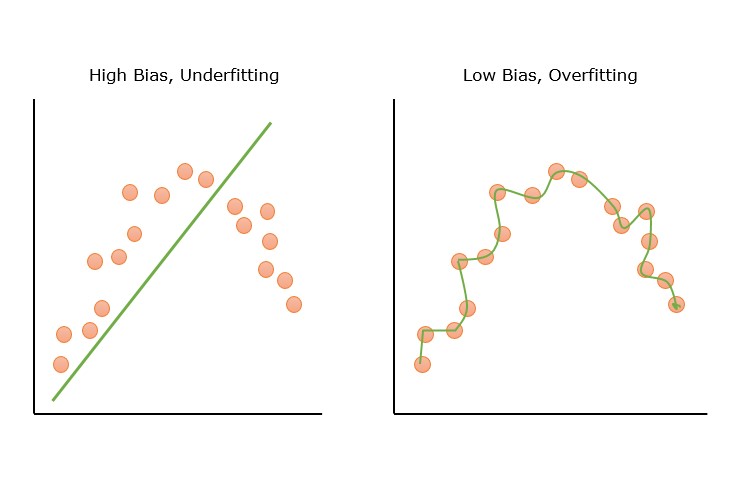
模型中偏差的示例

一个试图拟合非线性数据的线性回归模型将显示高偏差。一些高偏差模型的示例包括线性回归和逻辑回归。一些低偏差模型的示例包括决策树、K近邻和支持向量机。

偏差对模型性能的影响

高偏差会导致训练和测试数据集上的性能低下。高偏差模型将无法推广到新的、未见的数据。

什么是方差？

方差是衡量给定观测集中数字相对于平均值的离散程度或分散程度的指标。它基本上衡量了一组数字相对于平均值的离散程度。在统计学和概率论中，方差被定义为随机变量与其样本均值偏差平方的期望值。

在机器学习中，方差是模型在不同数据集上的预测变化。方差显示了当数据略有变化时，模型预测的变化程度。如果模型在训练和测试数据上的准确率差异很大，则该模型具有高方差。

高方差模型甚至可以拟合训练数据中的噪声，但缺乏对新的、未见数据的泛化能力。

方差类型

• **高方差** - 高方差模型捕获噪声以及隐藏模式。这会导致**过拟合**。高方差模型显示出高训练准确率，但测试准确率低。高方差模型的一些特征包括模型过于复杂、过拟合、训练数据误差低以及测试数据误差高。
• **低方差** - 低方差模型无法捕获数据中隐藏的模式。当我们拥有非常少的数据或使用非常简单的模型时，可能会出现低方差。低方差会导致**欠拟合**。

下图显示了高方差和低方差示例的图形表示。

模型中方差的示例

一个具有许多分支的决策树，它完美地拟合训练数据，但没有正确地拟合测试数据，就是一个高方差的例子。高方差的例子：K近邻、决策树和支持向量机 (SVM)。

方差对模型性能的影响

高方差会导致模型在训练数据上表现良好，但在训练数据上表现不佳。在训练过程中，高方差模型对训练数据拟合得非常好，甚至将噪声作为实际模式捕获。具有高方差误差的模型被称为**过拟合**模型。

偏差-方差权衡

偏差-方差权衡是在由偏差引入的误差和由方差引入的误差之间找到平衡。随着模型复杂度的增加，偏差会降低，但方差会增加。但是，当我们降低模型复杂度时，偏差会增加，方差会降低。因此，我们需要在偏差和方差之间找到平衡，以便最小化总预测误差。

如果机器学习模型在训练中存在高偏差或高方差，则它在新的、未见的数据上将无法很好地执行。一个好的模型不应该同时具有高偏差或高方差。我们不能同时降低偏差和方差。当偏差降低时，方差会增加。因此，我们需要找到最佳的偏差和方差，以便使预测误差最小化。

在机器学习中，偏差-方差权衡非常重要，因为具有高偏差或高的模型。

图形表示

下图以图形方式表示了偏差和方差之间的权衡。

在上图中，X 轴表示模型复杂度，Y 轴表示预测误差。总误差是偏差误差和方差误差的总和。最佳区域显示了偏差和方差之间平衡的区域，展示了具有最小误差的最佳模型复杂度。

数学表示

机器学习模型中的预测误差可以用数学方式表示如下：

误差 = 偏差² + 方差 + 不可减少误差。

为了最小化模型预测误差，我们需要选择模型复杂度，以便在这两种误差之间达到平衡。

偏差-方差权衡的主要目标是找到最小化误差的偏差和方差（模型复杂度）的最佳值。

平衡偏差和方差的技术

有不同的技术可以平衡偏差和方差以实现最佳预测误差。

1. 减少高偏差

• 选择更复杂的模型 - 正如我们在上图中看到的，选择更复杂的模型可以减少模型预测的偏差误差。
• 添加更多特征 - 添加更多特征可以增加模型的复杂性，从而更好地捕捉隐藏模式，从而减少模型的偏差误差。
• 减少正则化 - 正则化可以防止过拟合，但在减少方差的同时，它也可能增加偏差。因此，减少正则化参数或完全去除正则化可以减少偏差误差。

2. 减少高方差

• 应用正则化技术 - 正则化技术会对复杂模型添加惩罚，最终导致模型复杂度降低。较不复杂的模型将显示较小的方差。
• 简化模型复杂度 - 较不复杂的模型将具有较低的方差。您可以通过使用更简单的算法来减少方差。
• 添加更多数据 - 向数据集中添加更多数据可以帮助模型更好地执行，从而显示出较小的方差。
• 交叉验证 - 交叉验证可用于通过比较数据集的训练集和验证集上的性能来识别过拟合。

使用 Python 的偏差和方差示例

让我们使用 Python 编程语言实现一些实际示例。我们在这里提供了四个示例。前三个示例显示了某种程度的高/低偏差或方差。第四个示例显示了偏差和方差的最佳值。

高偏差示例

以下是 Python 中的实现示例，说明如何使用波士顿房价数据集分析偏差和方差：

import numpy as np
import pandas as pd
from sklearn.datasets import load_boston

boston = load_boston()
X = boston.data
y = boston.target
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2,
random_state=42)
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

lr = LinearRegression()
lr.fit(X_train, y_train)

train_preds = lr.predict(X_train)
train_mse = mean_squared_error(y_train, train_preds)
print("Training MSE:", train_mse)

test_preds = lr.predict(X_test)
test_mse = mean_squared_error(y_test, test_preds)
print("Testing MSE:", test_mse)

输出

输出显示了线性回归模型的训练和测试均方误差 (MSE)。训练 MSE 为 21.64，测试 MSE 为 24.29，表明模型具有高偏差和中等方差。

Training MSE: 21.641412753226312
Testing MSE: 24.291119474973456

低偏差和高方差示例

让我们尝试一个多项式回归模型：

from sklearn.preprocessing import PolynomialFeatures

poly = PolynomialFeatures(degree=2)
X_train_poly = poly.fit_transform(X_train)
X_test_poly = poly.transform(X_test)

pr = LinearRegression()
pr.fit(X_train_poly, y_train)

train_preds = pr.predict(X_train_poly)
train_mse = mean_squared_error(y_train, train_preds)
print("Training MSE:", train_mse)

test_preds = pr.predict(X_test_poly)
test_mse = mean_squared_error(y_test, test_preds)
print("Testing MSE:", test_mse)

输出

输出显示了度数为 2 的多项式回归模型的训练和测试 MSE。训练 MSE 为 5.31，测试 MSE 为 14.18，表明与线性回归模型相比，该模型具有较低的偏差但较高的方差。

Training MSE: 5.31446956670908
Testing MSE: 14.183558207567042

低方差示例

为了减少方差，我们可以使用正则化技术，例如岭回归或套索回归。在下面的示例中，我们将使用岭回归：

from sklearn.linear_model import Ridge

ridge = Ridge(alpha=1)
ridge.fit(X_train_poly, y_train)

train_preds = ridge.predict(X_train_poly)
train_mse = mean_squared_error(y_train, train_preds)
print("Training MSE:", train_mse)

test_preds = ridge.predict(X_test_poly)
test_mse = mean_squared_error(y_test, test_preds)
print("Testing MSE:", test_mse)

输出

输出显示了 alpha=1 的岭回归模型的训练和测试 MSE。与多项式回归模型相比，训练 MSE 为 9.03，测试 MSE 为 13.88，表明该模型具有较低的方差但略高的偏差。

Training MSE: 9.03220937860839
Testing MSE: 13.882093755326755

最佳偏差和方差示例

我们可以进一步调整超参数 alpha 以找到偏差和方差之间的最佳平衡。让我们看一个例子：

from sklearn.model_selection import GridSearchCV

param_grid = {'alpha': np.logspace(-3, 3, 7)}
ridge_cv = GridSearchCV(Ridge(), param_grid, cv=5)
ridge_cv.fit(X_train_poly, y_train)

train_preds = ridge_cv.predict(X_train_poly)
train_mse = mean_squared_error(y_train, train_preds)
print("Training MSE:", train_mse)

test_preds = ridge_cv.predict(X_test_poly)
test_mse = mean_squared_error(y_test, test_preds)
print("Testing MSE:", test_mse)

输出

输出显示了具有最佳 alpha 值的岭回归模型的训练和测试 MSE。

Training MSE: 8.326082686584716
Testing MSE: 12.873907256619141

训练 MSE 为 8.32，测试 MSE 为 12.87，表明该模型在偏差和方差之间取得了良好的平衡。