机器学习 - K均值聚类

---

---

K均值算法可以概括为以下步骤：

• 初始化 - 选择 K 个随机数据点作为初始中心点。

• 分配 - 将每个数据点分配到最近的中心点。

• 重新计算 - 通过取每个簇中所有数据点的平均值来重新计算中心点。

• 重复 - 重复步骤 2-3，直到中心点不再移动或达到最大迭代次数。

K均值算法是一种简单高效的算法，可以处理大型数据集。但是，它也有一些局限性，例如它对初始中心点的敏感性、它倾向于收敛到局部最优解，以及它假设所有簇的方差相等。

Python 实现

Python 有几个库提供了各种机器学习算法的实现，包括 K均值聚类。让我们看看如何使用 scikit-learn 库在 Python 中实现 K均值算法。

步骤 1 - 导入所需库

要在 Python 中实现 K均值算法，我们首先需要导入所需的库。我们将分别使用 numpy 和 matplotlib 库进行数据处理和可视化，以及 scikit-learn 库用于 K均值算法。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

步骤 2 - 生成数据

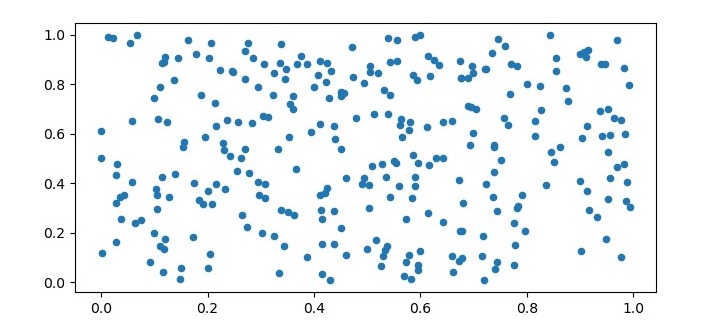
为了测试 K均值算法，我们需要生成一些示例数据。在本例中，我们将生成 300 个具有两个特征的随机数据点。我们也将可视化数据。

X = np.random.rand(300,2)

plt.figure(figsize=(7.5, 3.5))
plt.scatter(X[:, 0], X[:, 1], s=20, cmap='summer');
plt.show()

步骤 3 - 初始化 K均值

接下来，我们需要通过指定簇数 (K) 和最大迭代次数来初始化 K均值算法。

kmeans = KMeans(n_clusters=3, max_iter=100)

步骤 4 - 训练模型

初始化 K均值算法后，我们可以通过将数据拟合到算法中来训练模型。

kmeans.fit(X)

步骤 5 - 可视化簇

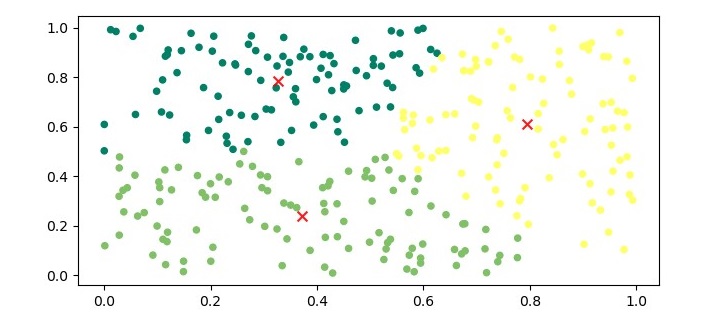
为了可视化簇，我们可以绘制数据点并根据其分配的簇对其进行着色。

plt.figure(figsize=(7.5, 3.5))
plt.scatter(X[:,0], X[:,1], c=kmeans.labels_, s=20, cmap='summer')
plt.scatter(kmeans.cluster_centers_[:,0], kmeans.cluster_centers_[:,1],
marker='x', c='r', s=50, alpha=0.9)
plt.show()

上述代码的输出将是一个图，其中数据点根据其分配的簇着色，并且中心点以红色“x”符号标记。

完整实现示例

以下是 Python 中 K均值聚类算法的完整实现示例：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

X = np.random.rand(300,2)
plt.figure(figsize=(7.5, 3.5))
plt.scatter(X[:, 0], X[:, 1], s=20, cmap='summer');
plt.show()

kmeans = KMeans(n_clusters=3, max_iter=100)
kmeans.fit(X)
plt.figure(figsize=(7.5, 3.5))
plt.scatter(X[:,0], X[:,1], c=kmeans.labels_, s=20, cmap='summer')
plt.scatter(kmeans.cluster_centers_[:,0], kmeans.cluster_centers_[:,1],
marker='x', c='r', s=50, alpha=0.9)
plt.show()

输出

执行此代码时，它将生成以下图作为输出：

K均值聚类的应用

K均值聚类是一种用途广泛的算法，在多个领域都有各种应用。在这里，我们重点介绍了一些重要的应用：

图像分割

K均值聚类可用于根据像素的颜色或纹理将图像分割成不同的区域。此技术广泛应用于计算机视觉应用中，例如物体识别、图像检索和医学影像。

客户细分

K均值聚类可用于根据客户的购买行为或人口统计特征将客户细分成不同的群体。此技术广泛应用于营销应用中，例如客户留存、忠诚度计划和目标广告。

异常检测

K均值聚类可用于通过识别不属于任何簇的数据点来检测数据集中是否存在异常。此技术广泛应用于欺诈检测、网络入侵检测和预测性维护。

基因组数据分析

K均值聚类可用于分析基因表达数据，以识别不同组的共同调控或共同表达的基因。此技术广泛应用于生物信息学应用中，例如药物发现、疾病诊断和个性化医疗。