
- 机器学习基础
- ML - 首页
- ML - 简介
- ML - 入门
- ML - 基本概念
- ML - 生态系统
- ML - Python库
- ML - 应用
- ML - 生命周期
- ML - 必备技能
- ML - 实现
- ML - 挑战与常见问题
- ML - 局限性
- ML - 真实案例
- ML - 数据结构
- ML - 数学基础
- ML - 人工智能
- ML - 神经网络
- ML - 深度学习
- ML - 获取数据集
- ML - 分类数据
- ML - 数据加载
- ML - 数据理解
- ML - 数据准备
- ML - 模型
- ML - 监督学习
- ML - 无监督学习
- ML - 半监督学习
- ML - 强化学习
- ML - 监督学习 vs. 无监督学习
- 机器学习数据可视化
- ML - 数据可视化
- ML - 直方图
- ML - 密度图
- ML - 箱线图
- ML - 相关矩阵图
- ML - 散点矩阵图
- 机器学习统计学
- ML - 统计学
- ML - 均值、中位数、众数
- ML - 标准差
- ML - 百分位数
- ML - 数据分布
- ML - 偏度和峰度
- ML - 偏差和方差
- ML - 假设
- ML中的回归分析
- ML - 回归分析
- ML - 线性回归
- ML - 简单线性回归
- ML - 多元线性回归
- ML - 多项式回归
- ML中的分类算法
- ML - 分类算法
- ML - 逻辑回归
- ML - K近邻算法 (KNN)
- ML - 朴素贝叶斯算法
- ML - 决策树算法
- ML - 支持向量机
- ML - 随机森林
- ML - 混淆矩阵
- ML - 随机梯度下降
- ML中的聚类算法
- ML - 聚类算法
- ML - 基于质心的聚类
- ML - K均值聚类
- ML - K中心点聚类
- ML - 均值漂移聚类
- ML - 层次聚类
- ML - 基于密度的聚类
- ML - DBSCAN聚类
- ML - OPTICS聚类
- ML - HDBSCAN聚类
- ML - BIRCH聚类
- ML - 亲和传播
- ML - 基于分布的聚类
- ML - 凝聚层次聚类
- ML中的降维
- ML - 降维
- ML - 特征选择
- ML - 特征提取
- ML - 后向剔除法
- ML - 前向特征构建
- ML - 高相关性过滤器
- ML - 低方差过滤器
- ML - 缺失值比率
- ML - 主成分分析
- 强化学习
- ML - 强化学习算法
- ML - 利用与探索
- ML - Q学习
- ML - REINFORCE算法
- ML - SARSA强化学习
- ML - 演员评论家方法
- 深度强化学习
- ML - 深度强化学习
- 量子机器学习
- ML - 量子机器学习
- ML - 使用Python的量子机器学习
- 机器学习杂项
- ML - 性能指标
- ML - 自动化工作流
- ML - 提升模型性能
- ML - 梯度提升
- ML - 自举汇聚 (Bagging)
- ML - 交叉验证
- ML - AUC-ROC曲线
- ML - 网格搜索
- ML - 数据缩放
- ML - 训练和测试
- ML - 关联规则
- ML - Apriori算法
- ML - 高斯判别分析
- ML - 成本函数
- ML - 贝叶斯定理
- ML - 精确率和召回率
- ML - 对抗性
- ML - 堆叠
- ML - 轮次
- ML - 感知器
- ML - 正则化
- ML - 过拟合
- ML - P值
- ML - 熵
- ML - MLOps
- ML - 数据泄露
- ML - 机器学习的货币化
- ML - 数据类型
- 机器学习资源
- ML - 快速指南
- ML - 速查表
- ML - 面试问题
- ML - 有用资源
- ML - 讨论
机器学习中的线性回归
机器学习中的线性回归被定义为一种统计模型,它分析因变量与一组给定的自变量之间的线性关系。变量之间的线性关系意味着,当一个或多个自变量的值发生变化(增加或减少)时,因变量的值也会相应地发生变化(增加或减少)。
在机器学习中,线性回归用于根据学习到的线性关系来预测新数据和未见数据的连续数值。它被用于预测建模、金融预测、风险评估等。
在本章中,我们将详细讨论以下主题:
- 什么是线性回归?
- 线性回归的类型
- 线性回归是如何工作的?
- 线性回归的假设函数
- 寻找最佳拟合线
- 线性回归的损失函数
- 用于优化的梯度下降法
- 线性回归的假设
- 线性回归的评估指标
- 线性回归的应用
- 线性回归的优点
- 线性回归的常见挑战
什么是线性回归?
线性回归是一种统计技术,它估计因变量和一个或多个自变量之间的线性关系。在机器学习中,线性回归被实现为一种监督学习方法。在机器学习中,标记数据集包含输入数据(特征)和输出标签(目标值)。对于机器学习中的线性回归,我们将特征表示为自变量,目标值表示为因变量。
为简化起见,请考虑以下数据(单个特征和单个目标):
| 平方英尺 (X) | 房价 (Y) |
|---|---|
| 1300 | 240 |
| 1500 | 320 |
| 1700 | 330 |
| 1830 | 295 |
| 1550 | 256 |
| 2350 | 409 |
| 1450 | 319 |
在上述数据中,目标房价是由 X 表示的因变量,而特征平方英尺是由 Y 表示的自变量。输入特征 (X) 用于预测目标标签 (Y)。因此,自变量也称为预测变量,因变量也称为响应变量。
因此,让我们将机器学习中的线性回归定义如下:
在机器学习中,线性回归使用线性方程来模拟因变量 (Y) 和一个或多个自变量 (Y) 之间的关系。
线性回归模型的主要目标是找到通过一组数据点的最佳拟合直线(通常称为回归线)。
回归线
显示因变量和自变量之间关系的直线称为回归线。
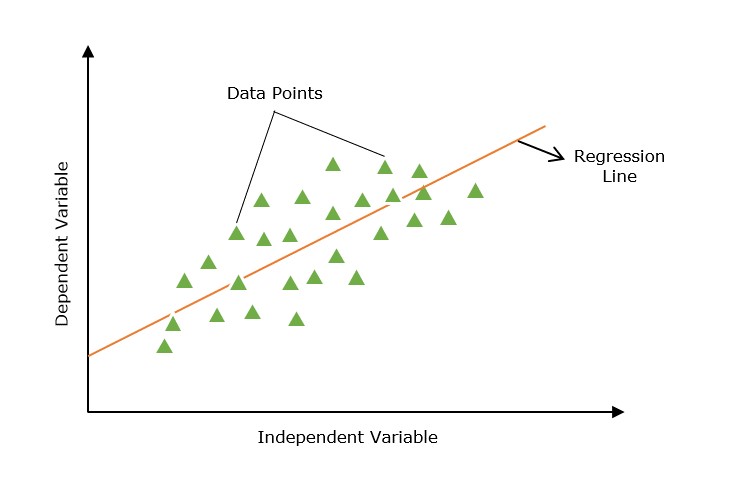
此外,线性关系可以是正的或负的,如下所述:
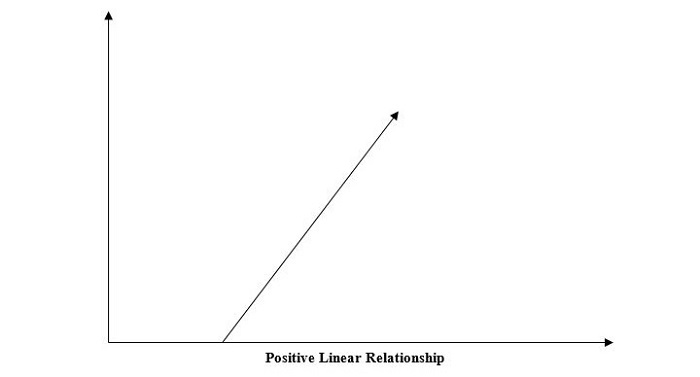
1. 正线性关系
如果自变量和因变量都增加,则线性关系称为正线性关系。这可以通过下图来理解:
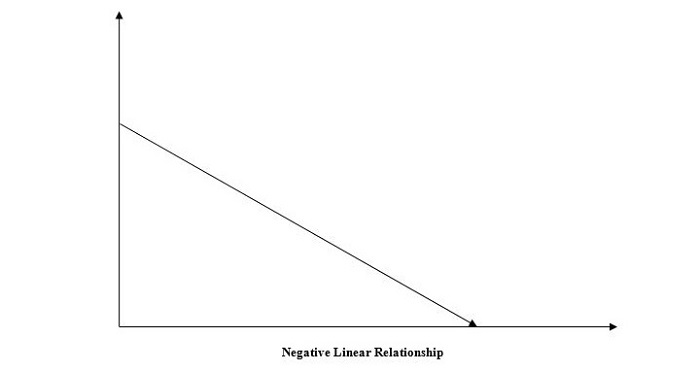
2. 负线性关系
如果自变量增加而因变量减少,则线性关系称为负线性关系。这可以通过下图来理解:
线性回归分为两种类型:“简单线性回归”和“多元线性回归”,我们将在本教程的接下来的两章中讨论。
线性回归的类型
线性回归分为以下两种类型:
- 简单线性回归
- 多元线性回归
1. 简单线性回归
简单线性回归是一种回归分析,其中使用单个自变量(也称为预测变量)来预测因变量。换句话说,它模拟因变量和单个自变量之间的线性关系。
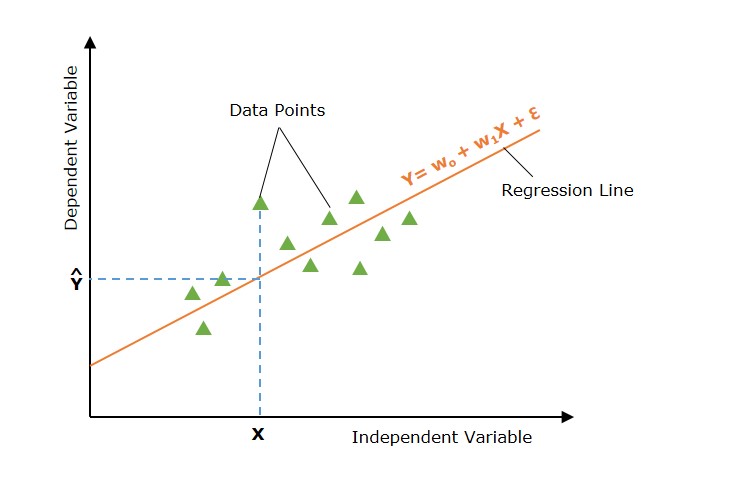
在上图中,直线代表简单线性回归线,其中 Ŷ 是预测值,X 是输入值。
数学上,这种关系可以建模为线性方程:
$$\mathrm{ Y = w_0 + w_1 X + \epsilon }$$
其中
- Y 是因变量(目标)。
- X 是自变量(特征)。
- w0 是线的 y 截距。
- w1 是线的斜率,表示 X 对 Y 的影响。
- ε 是误差项,捕获 X 未解释的 Y 中的可变性。
2. 多元线性回归
多元线性回归基本上是简单线性回归的扩展,它使用两个或多个特征来预测响应。
当处理多个自变量时,我们将简单线性回归扩展到多元线性回归。模型表示为:
多元线性回归将简单线性回归的概念扩展到多个自变量。模型表示为:
$$\mathrm{Y = w_0 + w_1 X_1 + w_2 X_2 + \dots + w_p X_p + \epsilon}$$
其中
- X1、X2、…、Xp 是自变量(特征)。
- w0、w1、…、wp 是这些变量的系数。
- ε 是误差项。
线性回归是如何工作的?
线性回归的主要目标是找到通过一组数据点的最佳拟合线,使实际值和预测值之间的差异最小化。那么这是如何实现的呢?这是通过估计参数 w0、w1 等来实现的。
机器学习中线性回归的工作原理可以分解为以下步骤:
- **假设** - 我们假设输入和输出之间存在线性关系。
- **成本函数** - 定义损失或成本函数。成本函数量化模型的预测误差。成本函数获取模型的预测值和实际值,并返回表示模型预测成本的单个标量值。
- **优化** - 通过更新模型的参数来优化(最小化)模型的成本函数。
它持续更新模型的参数,直到模型预测的成本或误差被优化(最小化)。
让我们更详细地讨论以上三个步骤 -
线性回归的假设函数
在线性回归问题中,我们假设输入特征 (X) 和预测值 (Ŷ) 之间存在线性关系。
该假设函数返回给定输入值的预测值。通常我们用 hw(X) 表示假设函数,它等于Ŷ。
简单线性回归的假设函数 -
$$\mathrm{\hat{Y} = w_0 + w_1 X}$$
多元线性回归的假设函数 -
$$\mathrm{\hat{Y} = w_0 + w_1 X_1 + w_2 X_2 + \dots + w_p X_p}$$
对于不同的参数值(权重),我们可以找到许多回归线。主要目标是找到最佳拟合线。让我们如下讨论 -
寻找最佳拟合线
我们在上面讨论过,不同的参数集会提供不同的回归线。但是,每条回归线都不能代表输入和输出值之间的最佳关系。主要目标是找到最佳拟合线。
如果实际值和预测值之间的误差最小,则称回归线为最佳拟合线。
下图显示了在输入数据点 X 处带有误差 (ε) 的回归线。误差是针对所有数据点计算的,我们的目标是最小化平均误差/损失。我们可以使用不同类型的损失函数,例如均方误差 (MSE)、平均绝对误差 (MAE)、L1 损失、L2 损失等。
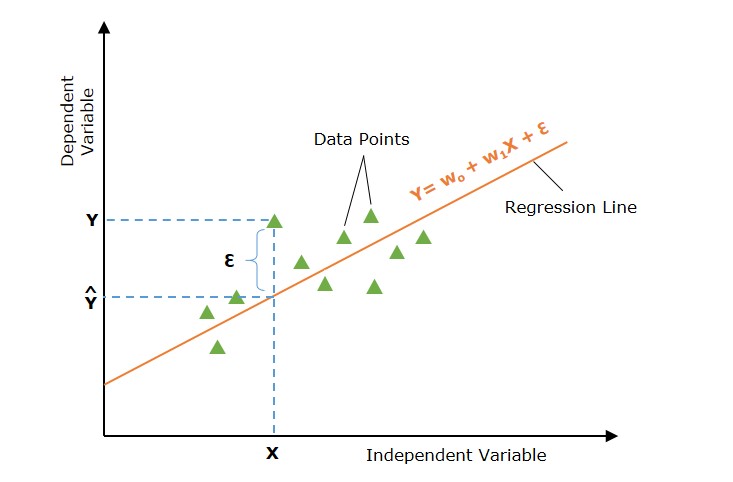
那么,我们如何最小化实际值和预测值之间的误差呢?让我们讨论一个重要的概念,即成本函数或损失函数。
线性回归的损失函数
可以使用损失函数或成本函数来量化实际值和预测值之间的误差。该成本函数采用模型的预测值和实际值,并返回一个表示模型预测成本的单个标量值。我们的主要目标是最小化成本函数。
最常用的成本函数是均方误差函数。
$$\mathrm{J(w_0, w_1) = \frac{1}{2n} \sum_{i=1}^{n} \left( Y_i - \hat{Y}_i \right)^2}$$
其中,
- n 是数据点的数量。
- Yi 是第 i 个数据点的观测值。
- \( \hat{Y}_i = w_0 + w_1 X_i \) 是第 i 个数据点的预测值。
用于优化的梯度下降法
现在我们已经定义了损失函数。下一步是最小化它并找到参数或权重的最优值。找到参数的最优值以使损失或误差最小化的过程称为模型优化。
梯度下降是线性回归最常用的优化技术之一。
为了找到参数的最优值,经常使用梯度下降法,尤其是在数据集很大的情况下。梯度下降法迭代地调整参数,使其沿成本函数最陡峭下降的方向移动。
参数更新由下式给出
$$\mathrm{w_0 = w_0 - \alpha \frac{\partial J}{\partial w_0}}$$
$$\mathrm{w_1 = w_1 - \alpha \frac{\partial J}{\partial w_1}}$$
其中 α 是学习率,偏导数为
$$\mathrm{\frac{\partial J}{\partial w_0} = -\frac{1}{n} \sum_{i=1}^{n} \left( Y_i - \hat{Y}_i \right)}$$
$$\mathrm{\frac{\partial J}{\partial w_1} = -\frac{1}{n} \sum_{i=1}^{n} \left( Y_i - \hat{Y}_i \right) X_i}$$
这些梯度用于更新参数,直到达到收敛(即,当 \( w_0 \) 和 \( w_1 \) 的变化变得可以忽略不计)。
线性回归的假设
以下是线性回归模型对数据集做出的某些假设 -
多重共线性 - 线性回归模型假设数据中几乎没有或没有多重共线性。基本上,当自变量或特征之间存在依赖关系时,就会发生多重共线性。
自相关 - 线性回归模型的另一个假设是数据中几乎没有或没有自相关。基本上,当残差误差之间存在依赖关系时,就会发生自相关。
变量之间的关系 - 线性回归模型假设响应变量和特征变量之间的关系必须是线性的。
违反这些假设会导致偏差或效率低下的估计。必须验证这些假设以确保模型的准确性。
线性回归的评估指标
为了评估线性回归模型的性能,使用了几个评估指标 -
R 平方 (R2) - 它衡量因变量中可由自变量预测的方差比例。
$$\mathrm{ R^2 = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \bar{y})^2} }$$
均方误差 (MSE) - 它衡量预测值和实际值之间平方差之和的平均值。
$$\mathrm{ \text{MSE} = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2 }$$
均方根误差 (RMSE) - 它衡量 MSE 的平方根。
$$\mathrm{ \text{RMSE} = \sqrt{\text{MSE}} }$$
平均绝对误差 (MAE) - 它衡量预测值和实际值之间差异的绝对值之和的平均值。
$$\mathrm{ \text{MAE} = \frac{1}{n} \sum_{i=1}^n |y_i - \hat{y}_i| }$$
线性回归的应用
1. 预测建模
线性回归广泛用于预测建模。例如,在房地产中,根据大小、位置和卧室数量等特征预测房价可以帮助买家、卖家和房地产经纪人做出明智的决定。
2. 特征选择
在多元线性回归中,分析系数有助于特征选择。系数较小或为零的特征可能被认为不太重要,可以删除以简化模型。
3. 金融预测
在金融领域,线性回归模型可以预测股票价格、经济指标和市场趋势。准确的预测可以指导投资策略和财务规划。
4. 风险管理
线性回归通过对风险因素和财务指标之间的关系建模来帮助进行风险评估。例如,在保险中,它可以对投保人特征与索赔金额之间的关系建模。
线性回归的优点
- 可解释性 - 线性回归易于理解,这在解释模型如何做出决策时非常有用。
- 速度 - 线性回归比许多其他机器学习算法训练速度更快。
- 预测分析 - 线性回归是预测分析的基础组成部分。
- 线性关系 - 线性回归是一种强大的统计方法,用于查找变量之间的线性关系。
- 简单性 - 线性回归易于实现和解释。
- 效率 - 线性回归计算效率高。
线性回归的常见挑战
1. 过拟合
过拟合是指回归模型在训练数据上表现良好,但在测试数据上缺乏泛化能力的情况。过拟合会导致对新的、未见过的数据的预测效果差。
2. 多重共线性
当因变量(预测变量或特征变量)相关时,这种情况称为多重共线性。在这种情况下,参数(系数)的估计值可能不稳定。
3. 离群值及其影响
离群值会导致回归线成为大多数数据点的糟糕拟合。
多项式回归:线性回归的替代方法
多项式线性回归是一种回归分析,其中自变量和因变量之间的关系被建模为 n 次多项式函数。多项式回归允许捕获变量之间比简单和多元线性回归中的线性关系更复杂的关系。