机器学习中的回归分析

---

---

什么是回归分析？

在机器学习中，回归分析是一种统计技术，它根据自变量和因变量之间的关系来预测连续的数值。回归分析的主要目标是绘制一条最适合数据的线或曲线，并估计一个变量如何影响另一个变量。

回归分析是机器学习中的一个基本概念，它被用于许多应用中，例如预测、预测分析等。

在机器学习中，回归是一种监督学习类型。基于回归的任务的关键目标是预测输出标签或响应，这些是给定输入数据的连续数值。输出将基于模型在训练阶段学到的内容。

基本上，回归模型使用输入数据特征（自变量）及其对应的连续数值输出值（因变量或结果变量）来学习输入和相应输出之间特定的关联。

回归分析中使用的术语

在深入了解之前，让我们了解一下回归分析中使用的一些基本术语。以下是一些重要的术语：

• 自变量 - 这些变量用于预测因变量的值。这些也被称为预测变量。在数据集中，这些表示为特征。
• 因变量 - 这些是我们想要预测其值的变量。这些是回归分析中的主要因素。在数据集中，这些表示为目标变量
• 回归线 - 它是回归器绘制以最好地拟合数据点的直线或曲线。
• 过拟合和欠拟合 - 过拟合是指回归模型在训练数据集上运行良好，但在测试数据集上运行不佳。它也被称为高方差问题。欠拟合是指模型在训练数据集上运行不佳。它也被称为高偏差问题。
• 异常值 - 这些是不符合数据其余部分模式的数据点。它们是数据集中极高或极低的值。
• 多重共线性 - 当自变量（特征）之间存在依赖关系时，就会发生多重共线性。

回归是如何工作的？

机器学习中的回归是一种监督学习。基本上，回归是一种统计技术，它寻找因变量和自变量之间的关系。为了在机器学习中实现回归，回归算法使用带标签的数据集进行训练。数据集包含特征（自变量）和目标值（因变量）。

在训练阶段，回归算法学习自变量（预测变量）和因变量（目标）之间的关系。

回归模型根据训练期间学习到的预测变量和目标之间的关系预测新值。

机器学习中的回归类型

通常，回归方法的分类是根据三个指标进行的：自变量的数量、因变量的类型以及回归线的形状。

机器学习中使用了许多回归技术。但是，以下是一些常用的回归类型：

• 线性回归
• 逻辑回归
• 多项式回归
• Lasso回归
• 岭回归
• 决策树回归
• 随机森林回归
• 支持向量回归

让我们详细讨论机器学习中每种类型的回归。

1. 线性回归

线性回归是机器学习中最常用的回归模型。线性回归可以定义为分析因变量与给定一组自变量之间线性关系的统计模型。变量之间的线性关系意味着当一个或多个自变量的值发生变化（增加或减少）时，因变量的值也会相应地发生变化（增加或减少）。

线性回归进一步分为两个子类别：简单线性回归和多元线性回归（也称为多元线性回归）。

在简单线性回归中，单个自变量（或预测变量）用于预测因变量。

在数学上，简单线性回归可以表示如下：

$$Y=mX+b$$

其中，

• Y是我们试图预测的因变量。
• X是我们用来进行预测的自变量。
• m是回归线的斜率，它表示X对Y的影响。
• b是一个常数，称为Y截距。如果X = 0，则Y将等于b。

在多元线性回归中，多个自变量用于预测因变量。

我们将在后续章节中更详细地学习线性回归。

2. 逻辑回归

逻辑回归是一种流行的机器学习算法，用于预测事件发生的概率。

逻辑回归是一种广义线性模型，其中目标变量服从伯努利分布。逻辑回归使用逻辑函数或Logit函数来学习自变量（预测变量）和因变量（目标）之间的关系。

它将因变量映射为自变量的S形函数。S形函数产生0到1之间的概率。概率值用于估计因变量的值。

它主要用于二元分类问题，其中目标变量是具有两个类别的分类变量。它根据输入特征对目标变量的概率进行建模，并预测概率最高的类别。

3. 多项式回归

多项式线性回归 是一种回归分析，其中自变量和因变量之间的关系被建模为 n 次多项式函数。与简单线性回归和多元线性回归中的线性关系相比，多项式回归允许捕获变量之间更复杂的关系。

多项式回归是最广泛使用的非线性回归之一。它非常有用，因为它可以模拟预测变量和目标变量之间的非线性关系，并且对异常值更敏感。

4. Lasso 回归

Lasso 回归是一种正则化技术，它使用惩罚来防止过拟合并提高回归模型的准确性。它执行 L1 正则化。它通过添加等于系数绝对值之和的惩罚（收缩量）来修改损失函数。

Lasso 回归通常用于处理高维和高度相关的数据。

5. Ridge 回归

Ridge 回归是一种统计技术，用于机器学习中防止线性回归模型过拟合。它用作正则化技术，执行 L2 正则化。它通过添加等于系数大小平方和的惩罚（收缩量）来修改损失或代价函数。

Ridge 回归有助于降低模型复杂度并提高预测准确性。它在开发许多具有高权重的参数时很有用。它也适用于特征变量数量多于观测数量的数据集。

它还修正了回归分析中的多重共线性。当自变量相互依赖时，就会发生多重共线性。

6. 决策树回归

决策树回归使用决策树算法来预测数值。决策树算法是一种监督式机器学习算法，可用于分类和回归。

它用于预测数值或连续变量。它的工作原理是根据输入特征的值将数据分成更小的子集，并为每个子集分配一个数值。因此，它逐步地开发了一个决策树。

该树拟合局部线性回归以近似曲线，每个叶子表示一个数值。该算法试图减少每个子节点的均方误差，该误差衡量预测与原始目标的偏差程度。

决策树回归可用于预测股票价格或客户行为等。

7. 随机森林回归

随机森林回归是一种监督式机器学习算法，它使用决策树的集成来预测连续的目标变量。它使用一种装袋技术，该技术涉及随机选择训练数据的子集来构建较小的决策树。这些较小的模型组合在一起形成一个随机森林模型，该模型输出单个预测值。

该技术通过结合多个决策树的预测来提高准确性和降低方差。

8. 支持向量机回归

支持向量机回归 (SVR) 是一种机器学习算法，它使用支持向量机来解决回归问题。它可以学习输入数据（特征变量）和输出数据（目标值）之间的非线性关系。

支持向量机回归具有许多优点。它可以处理数据集中的线性关系和非线性关系。它对异常值具有鲁棒性。它具有较高的预测精度。

如何选择最佳回归模型？

您可以考虑性能指标、模型复杂度、可解释性等因素来选择最佳回归模型。使用均方误差 (MSE)、平均绝对误差 (MAE)、R 平方等指标评估模型性能。比较不同模型（如线性回归、决策树、随机森林等）的性能，并选择具有最高性能指标、最低复杂度和最佳可解释性的模型。

回归评估指标

回归模型的常用评估指标 -

• 平均绝对误差 (MAE) - 它是预测值与真实值之间绝对差值的平均值。
• 均方误差 (MSE) - 它是实际值与估计值之间差值的平方的平均值。
• 中位数绝对误差 - 它是预测值与真实值之间绝对差值的中位数。
• 均方根误差 (RMSE) - 它是均方误差 (MSE) 的平方根值。
• R²（决定系数）得分 - 最佳可能得分是 1.0，它可以为负数（因为模型可以任意变差）。
• 平均绝对百分比误差 (MAPE) - 它是平均绝对误差 (MAE) 的百分比等价物。

回归在机器学习中的应用

ML 回归算法的应用如下 -

预测或预测分析 - 回归的重要用途之一是预测或预测分析。例如，我们可以预测 GDP、油价，或者简单地说，随时间推移而变化的定量数据。

优化 - 我们可以借助回归优化业务流程。例如，商店经理可以创建统计模型来了解顾客高峰时间。

错误修正 - 在业务中，做出正确的决策与优化业务流程同等重要。回归可以帮助我们做出正确的决策以及修正已经实施的决策。

经济学 - 它是经济学中使用最广泛的工具。我们可以使用回归来预测供给、需求、消费、存货投资等。

金融 - 金融公司始终对最小化风险投资组合感兴趣，并希望了解影响客户的因素。所有这些都可以借助回归模型进行预测。

使用 Python 构建回归器

可以使用 Python 从头开始构建回归器模型。Scikit-learn 是一个用于机器学习的 Python 库，也可以用于在 Python 中构建回归器。

在以下示例中，我们将构建一个基本的回归模型，该模型将拟合一条线到数据，即线性回归器。在 Python 中构建回归器的必要步骤如下 -

步骤 1：导入必要的 Python 包

要使用 scikit-learn 构建回归器，我们需要导入它以及其他必要的包。我们可以使用以下脚本导入它 -

import numpy as np
from sklearn import linear_model
import sklearn.metrics as sm
import matplotlib.pyplot as plt

步骤 2：导入数据集

导入必要的包后，我们需要一个数据集来构建回归预测模型。我们可以从 sklearn 数据集中导入它，也可以根据我们的需要使用其他数据集。我们将使用我们保存的输入数据。我们可以使用以下脚本导入它 -

input = r'C:\linear.txt'

接下来，我们需要加载此数据。我们使用np.loadtxt函数加载它。

input_data = np.loadtxt(input, delimiter=',')
X, y = input_data[:, :-1], input_data[:, -1]

步骤 3：将数据组织成训练集和测试集

由于我们需要在未见过的数据上测试我们的模型，因此我们将数据集分成两部分：训练集和测试集。以下命令将执行此操作 -

training_samples = int(0.6 * len(X))
testing_samples = len(X) - num_training
X_train, y_train = X[:training_samples], y[:training_samples]
X_test, y_test = X[training_samples:], y[training_samples:]

步骤 4：模型评估和预测

将数据划分为训练集和测试集后，我们需要构建模型。我们将为此使用 Scikit-learn 的 LineaRegression() 函数。以下命令将创建一个线性回归器对象。

reg_linear = linear_model.LinearRegression()

接下来，使用训练样本训练此模型，如下所示 -

reg_linear.fit(X_train, y_train)

现在，最后我们需要使用测试数据进行预测。

y_test_pred = reg_linear.predict(X_test)

步骤 5：绘图和可视化

预测后，我们可以使用以下脚本绘制和可视化它 -

plt.scatter(X_test, y_test, color = 'red')
plt.plot(X_test, y_test_pred, color = 'black', linewidth = 2)
plt.xticks(())
plt.yticks(())
plt.show()

输出

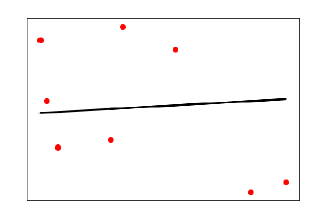
在上面的输出中，我们可以看到数据点之间的回归线。

步骤 6：性能计算

我们还可以使用各种性能指标来计算回归模型的性能，如下所示。

print("Regressor model performance:")
print("Mean absolute error(MAE) =", round(sm.mean_absolute_error(y_test, y_test_pred), 2))
print("Mean squared error(MSE) =", round(sm.mean_squared_error(y_test, y_test_pred), 2))
print("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2))
print("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred), 2))
print("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))

输出

Regressor model performance:
Mean absolute error(MAE) = 1.78
Mean squared error(MSE) = 3.89
Median absolute error = 2.01
Explain variance score = -0.09
R2 score = -0.09