
- 机器学习基础
- ML - 首页
- ML - 简介
- ML - 入门
- ML - 基本概念
- ML - 生态系统
- ML - Python 库
- ML - 应用
- ML - 生命周期
- ML - 所需技能
- ML - 实现
- ML - 挑战与常见问题
- ML - 限制
- ML - 现实生活中的例子
- ML - 数据结构
- ML - 数学
- ML - 人工智能
- ML - 神经网络
- ML - 深度学习
- ML - 获取数据集
- ML - 分类数据
- ML - 数据加载
- ML - 数据理解
- ML - 数据准备
- ML - 模型
- ML - 监督学习
- ML - 无监督学习
- ML - 半监督学习
- ML - 强化学习
- ML - 监督学习与无监督学习
- 机器学习数据可视化
- ML - 数据可视化
- ML - 直方图
- ML - 密度图
- ML - 箱线图
- ML - 相关矩阵图
- ML - 散点矩阵图
- 机器学习统计学
- ML - 统计学
- ML - 均值、中位数、众数
- ML - 标准差
- ML - 百分位数
- ML - 数据分布
- ML - 偏度和峰度
- ML - 偏差和方差
- ML - 假设
- ML中的回归分析
- ML - 回归分析
- ML - 线性回归
- ML - 简单线性回归
- ML - 多元线性回归
- ML - 多项式回归
- ML中的分类算法
- ML - 分类算法
- ML - 逻辑回归
- ML - K近邻算法(KNN)
- ML - 朴素贝叶斯算法
- ML - 决策树算法
- ML - 支持向量机
- ML - 随机森林
- ML - 混淆矩阵
- ML - 随机梯度下降
- ML中的聚类算法
- ML - 聚类算法
- ML - 基于中心点的聚类
- ML - K均值聚类
- ML - K中心点聚类
- ML - 均值漂移聚类
- ML - 层次聚类
- ML - 基于密度的聚类
- ML - DBSCAN聚类
- ML - OPTICS聚类
- ML - HDBSCAN聚类
- ML - BIRCH聚类
- ML - 亲和传播
- ML - 基于分布的聚类
- ML - 凝聚层次聚类
- ML中的降维
- ML - 降维
- ML - 特征选择
- ML - 特征提取
- ML - 后退消除法
- ML - 前向特征构建
- ML - 高相关性过滤器
- ML - 低方差过滤器
- ML - 缺失值比率
- ML - 主成分分析
- 强化学习
- ML - 强化学习算法
- ML - 利用与探索
- ML - Q学习
- ML - REINFORCE算法
- ML - SARSA强化学习
- ML - 演员-评论家方法
- 深度强化学习
- ML - 深度强化学习
- 量子机器学习
- ML - 量子机器学习
- ML - 使用Python的量子机器学习
- 机器学习杂项
- ML - 性能指标
- ML - 自动工作流
- ML - 提升模型性能
- ML - 梯度提升
- ML - 自举汇聚(Bagging)
- ML - 交叉验证
- ML - AUC-ROC曲线
- ML - 网格搜索
- ML - 数据缩放
- ML - 训练和测试
- ML - 关联规则
- ML - Apriori算法
- ML - 高斯判别分析
- ML - 成本函数
- ML - 贝叶斯定理
- ML - 精确率和召回率
- ML - 对抗性
- ML - 堆叠
- ML - 时期
- ML - 感知器
- ML - 正则化
- ML - 过拟合
- ML - P值
- ML - 熵
- ML - MLOps
- ML - 数据泄露
- ML - 机器学习的货币化
- ML - 数据类型
- 机器学习 - 资源
- ML - 快速指南
- ML - 速查表
- ML - 面试问题
- ML - 有用资源
- ML - 讨论
机器学习中的简单线性回归
什么是简单线性回归?
简单线性回归是一种统计学和监督学习方法,其中使用单个自变量(也称为预测变量)来预测因变量。换句话说,它模拟因变量与单个自变量之间的线性关系。
机器学习中的简单线性回归是线性回归的一种类型。当线性回归算法处理单个自变量时,称为简单线性回归。当存在多个自变量(特征变量)时,称为多元线性回归。
自变量
数据集中特征输入称为自变量。简单线性回归中只有一个自变量。自变量也称为预测变量,因为它用于预测目标值。它绘制在水平轴上。
因变量
数据集中目标值称为因变量。它也称为响应变量或预测变量。它绘制在垂直轴上。
回归线
在简单线性回归中,回归线是一条最适合数据点的直线,用于显示因变量和自变量之间的关系。
图形表示
下图描述了简单线性回归模型 -
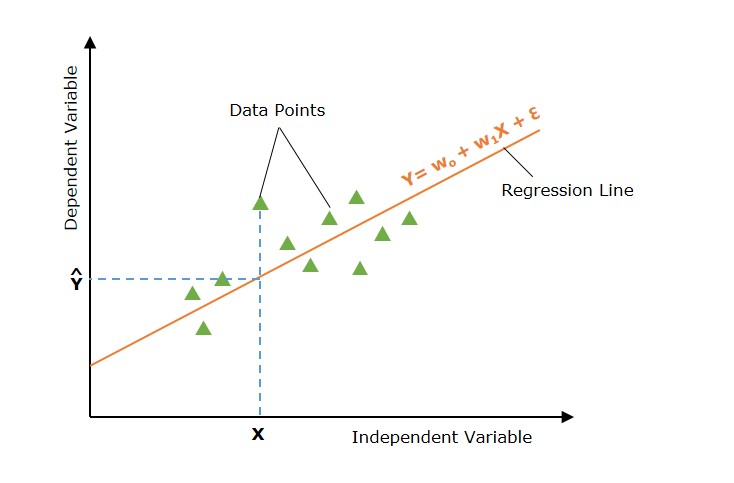
在上图中,直线表示简单线性回归线,其中Ŷ是预测值,Y是因变量(目标),X是自变量(输入)。
简单线性回归模型
机器学习中的简单线性回归模型可以用以下数学方程式表示 -
$$\mathrm{ Y = w_0 + w_1 X + \epsilon }$$
其中
- Y 是因变量(目标)。
- X 是自变量(特征)。
- w0 是线的 y 截距。
- w1 是线的斜率,表示 X 对 Y 的影响。
- ε 是误差项,捕获 X 未解释的 Y 中的变化。
简单线性回归如何工作?
简单线性回归的主要目的是找到穿过数据点并使实际值与预测值之间的差异最小化的最佳拟合线(直线)。
定义假设函数
在简单线性回归中,假设是因变量(输出/目标)和自变量(输入)之间存在线性关系。这种线性关系可以使用线性方程表示 -
$$\mathrm{\hat{Y} = w_0 + w_1 X}$$
使用参数 w0 和 w1 的不同值,存在多个线性方程(直线)。所有此类线性方程(所有直线)的集合称为假设空间。
现在,简单线性回归模型的主要目标是在假设空间(所有直线的集合)中找到最佳拟合线。
找到最佳拟合线
现在任务是找到最佳拟合线(回归线)。为此,我们定义一个成本函数或损失函数来衡量实际值与预测值之间的差异。
为了找到最佳拟合线,简单线性回归模型会初始化(使用默认值)回归线的参数。此回归线(使用初始化的参数)用于找到给定输入值的预测值。
简单线性回归的损失函数
现在使用输入值和预测值,我们计算损失函数。损失函数用于找到参数的最佳值。
损失函数找到输入值与预测值之间的差异。简单线性回归中使用了不同的损失函数,例如均方误差 (MSE)、平均绝对误差 (MEA)、R 平方等。最常用的损失函数是均方误差。
简单线性回归的损失函数(以均方误差表示)如下 -
$$\mathrm{J(w_0, w_1) = \frac{1}{2n} \sum_{i=1}^{n} \left( Y_i - \hat{Y}_i \right)^2}$$
优化
参数的最佳值是使成本函数最小化的那些值。找到最佳值是一个迭代过程,其中参数被迭代更新。
简单线性回归中应用了许多优化技术。梯度下降是一种简单且最常用的优化技术,用于简单线性回归。
具有最佳参数值的线性方程是最佳拟合线(回归线),它是简单线性回归问题的最终解决方案。此线用于预测新的和看不见的数据。
简单线性回归的假设
简单线性回归模型对数据集做出了一些假设。以下是一些假设 -
- 线性 - 此假设假设因变量和自变量之间的关系是线性的。这意味着随着自变量的变化,因变量线性变化。散点图将显示数据集中线性关系。
- 同方差性 - 对于所有观察值,残差的方差相同。此假设与残差平方有关。
- 独立性 - 示例(观察值或 X 和 Y 对)是独立的。数据中不存在共线性,因此残差不会相关。要检查这一点,我们查看残差与拟合的散点图。
- 正态性 - 模型残差服从正态分布。残差是实际值和预测值之间的差异。为了检查正态性,我们检查残差的直方图。直方图应该近似服从正态分布。
使用 Python 实现简单线性回归算法
为了实现简单线性回归算法,我们使用一个包含两个变量的数据集:工作年限(自变量)和薪资(因变量)。
这里,我们使用以下数据集。数据集包含 30 个数据点的示例。您可以创建一个 CSV 文件并将这些数据点存储在其中。
Salary_Data.csv
| 工作年限 | 薪资 |
|---|---|
| 1.1 | 39343 |
| 1.3 | 46205 |
| 1.5 | 37731 |
| 2 | 43525 |
| 2.2 | 39891 |
| 2.9 | 56642 |
| 3 | 60150 |
| 3.2 | 54445 |
| 3.2 | 64445 |
| 3.7 | 57189 |
| 3.9 | 63218 |
| 4 | 55794 |
| 4 | 56957 |
| 4.1 | 57081 |
| 4.5 | 61111 |
| 4.9 | 67938 |
| 5.1 | 66029 |
| 5.3 | 83088 |
| 5.9 | 81363 |
| 6 | 93940 |
| 6.8 | 91738 |
| 7.1 | 98273 |
| 7.9 | 101302 |
| 8.2 | 113812 |
| 8.7 | 109431 |
| 9 | 105582 |
| 9.5 | 116969 |
| 9.6 | 112635 |
| 10.3 | 122391 |
| 10.5 | 121872 |
此实现的目的是什么?
构建这个简单线性回归模型的目的是确定哪条线最能代表这两个变量之间的关系。
以下是使用 Python 实现简单线性回归模型的步骤:
步骤 1:数据准备
数据准备或预处理是第一步。我们有一个名为“Salary_Data.csv”的 CSV 文件作为数据集,如上所述。
在导入数据集和构建简单线性回归模型之前,我们需要导入 Python 库。
import numpy as np import matplotlib.pyplot as plt import pandas as pd
加载数据集
dataset = pd.read_csv('Salary_Data.csv')
然后必须从提供的数据集中提取因变量 (X) 和自变量 (Y)。工作年限(YearsExperience)是自变量,Salary 是因变量。
X = dataset.iloc[:, :-1].values y = dataset.iloc[:, -1].values
让我们检查数据集的前五个示例。
print(dataset.head())
输出
0 1.1 39343.0 1 1.3 46205.0 2 1.5 37731.0 3 2.0 43525.0 4 2.2 39891.0
让我们检查数据集是否线性
plt.scatter(X, y, color="green")
plt.title("Salary vs Experience")
plt.xlabel("Years of Experience")
plt.ylabel("Salary (INR)")
plt.show()
输出
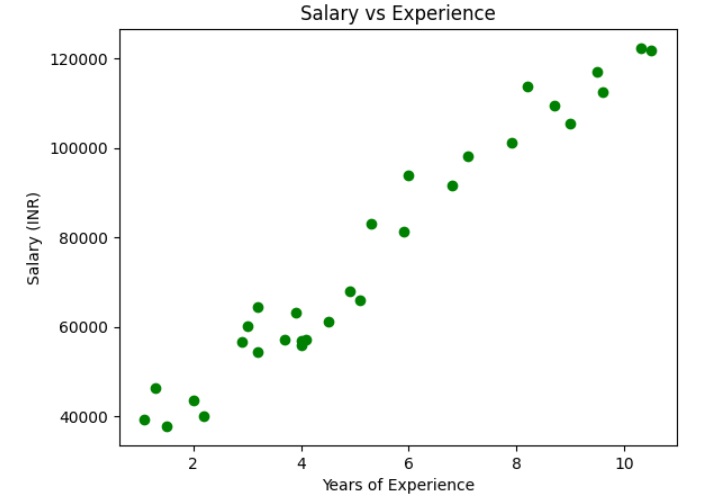
上图显示自变量和因变量之间存在线性关系。因此,我们可以对数据集应用简单线性回归,以找到这些变量之间最佳的关系。
将数据集分成训练集和测试集
然后将训练集和测试集分成两组。我们将使用 80% 的观测值作为训练集,20% 的观测值作为测试集,从我们拥有的总共 30 个观测值中。因此,训练集中将有 24 个观测值,测试集中将有 6 个观测值。我们将数据集分成训练集和测试集,以便我们可以使用一组进行训练,另一组进行测试我们的模型。
# Split the dataset into training and testing sets from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
这里,X_train 表示训练数据的输入特征,y_train 表示输出变量(目标变量)。
步骤 2:模型训练(将简单线性回归拟合到训练集)
下一步是用训练数据集拟合我们的模型。我们将使用 scikit-learn 的 LinearRegression 类在训练数据上训练一个简单线性回归模型。代码如下:
from sklearn.linear_model import LinearRegression # Create a linear regression object regressor= LinearRegression() regressor.fit(X_train, y_train)
fit() 方法用于将线性回归对象(regressor)拟合到训练数据。模型学习预测变量 (X_train) 和目标变量 (y_train) 之间的关系。
步骤 3:模型测试
模型训练完成后,我们可以使用它对测试数据进行预测。代码如下:
y_pred = regressor.predict(X_test)
df = pd.DataFrame({'Actual Values':y_test, 'Predicted Values':y_pred})
print(df)
输出
Actual Values Predicted Values 0 60150.0 54093.648425 1 93940.0 82416.119864 2 57081.0 64478.554619 3 116969.0 115459.003211 4 56957.0 63534.472238 5 121872.0 124899.827024
以上输出显示了测试集中薪资的实际值和预测值。
这里,X_test 表示测试数据的输入特征,y_pred 表示预测的输出变量(目标变量)。
同样,您可以使用训练数据测试模型。
y_pred = regressor.predict(X_train)
df = pd.DataFrame({'Real Values':y_test, 'Predicted Values':y_pred})
print(df)
输出
Real Values Predicted Values 0 57189.0 60702.225094 1 64445.0 55981.813188 2 63218.0 62590.389857 3 122391.0 123011.662261 4 91738.0 89968.778915 5 43525.0 44652.824612 6 61111.0 68254.884145 7 56642.0 53149.566044 8 66029.0 73919.378433 9 83088.0 75807.543195 10 46205.0 38044.247943 11 109431.0 107906.344160 12 98273.0 92801.026059 13 37731.0 39932.412705 14 54445.0 55981.813188 15 39891.0 46540.989374 16 101302.0 100353.685109 17 55794.0 63534.472238 18 81363.0 81472.037483 19 39343.0 36156.083180 20 113812.0 103185.932253 21 67938.0 72031.213670 22 112635.0 116403.085592 23 105582.0 110738.591304
步骤 4:模型评估
我们需要评估模型的性能以确定其准确性。我们将使用均方误差 (MSE)、均方根误差 (RMSE)、平均绝对误差 (MAE) 和决定系数 (R^2) 作为评估指标。代码如下:
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import r2_score
# get the predicted values for test dat
y_pred = regressor.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print("mse", mse)
rmse = mean_squared_error(y_test, y_pred, squared=False)
print("rsme", rmse)
mae = mean_absolute_error(y_test, y_pred)
print("mae", mae)
r2 = r2_score(y_test, y_pred)
print("r2", r2)
输出
mse: 46485664.99327367 rsme: 6818.0396737826095 mae: 6015.513730219523 r2: 0.9399326805390613
这里,y_test 表示测试数据的实际输出变量。
步骤 5:可视化训练集结果(带回归线)
现在,让我们可视化训练集上的结果和回归线。
我们使用散点图绘制训练集中实际值(输入和目标值)。我们还绘制了一条直线(回归线)表示训练集的实际值(输入)和预测值。
y_pred = regressor.predict(X_train)
plt.scatter(X_train, y_train, color="green", label="training data points (actual)")
plt.scatter(X_train, y_pred, color="blue",label="training data points (predicted)")
plt.plot(X_train, y_pred, color="red")
plt.title("Salary vs Experience (Training Dataset)")
plt.xlabel("Years of Experience")
plt.ylabel("Salary(In Rupees)")
plt.legend()
plt.show()
输出
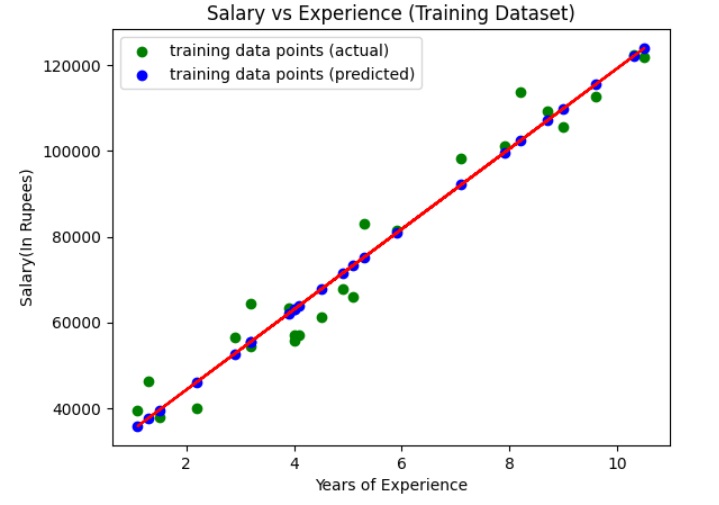
上图显示了回归线(红色直线)、实际值(绿色)和训练集的预测值(蓝色)。
步骤 6:可视化测试集结果(带回归线)
现在,让我们可视化测试集上的结果和回归线。
我们使用散点图绘制测试集中实际值(输入和目标值)。我们还绘制了一条直线(回归线)表示测试集的实际值(输入)和预测值。
y_pred = regressor.predict(X_test)
plt.scatter(X_test, y_test, color="green", label="test data points (actual)")
plt.scatter(X_test, y_pred, color="blue",label="test data points (predicted)")
plt.plot(X_test, y_pred, color="red")
plt.title("Salary vs Experience (Test Dataset)")
plt.xlabel("Years of Experience")
plt.ylabel("Salary(In Rupees)")
plt.legend()
plt.show()
输出
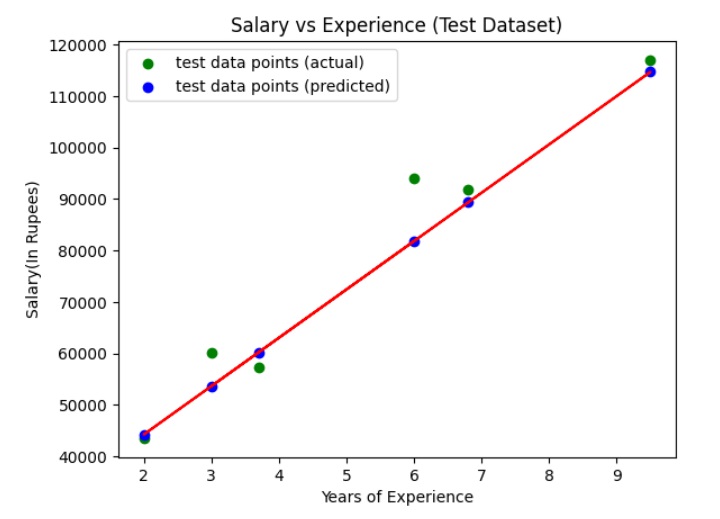
上图显示了回归线(红色直线)、实际值(绿色)和测试集的预测值(蓝色)。