机器学习 - 特征提取

特征提取通常用于图像处理、语音识别、自然语言处理和其他应用，在这些应用中，原始数据是高维的并且难以处理。

示例

以下是如何使用主成分分析 (PCA) 对鸢尾花数据集进行特征提取的 Python 示例：

# Import necessary libraries and dataset
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# Load the dataset
iris = load_iris()

# Perform feature extraction using PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(iris.data)

# Visualize the transformed data
plt.figure(figsize=(7.5, 3.5))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=iris.target)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.show()

在此代码中，我们首先导入必要的库，包括用于使用 PCA 进行特征提取的 sklearn 和用于可视化转换数据的 matplotlib。

接下来，我们使用 load_iris() 加载鸢尾花数据集。然后，我们使用 PCA() 进行特征提取并将组件数量设置为 2 (n_components=2)。这将输入数据的维度从 4 个特征减少到 2 个主成分。

然后，我们使用 fit_transform() 转换输入数据并将转换后的数据存储在 X_pca 中。最后，我们使用 plt.scatter() 可视化转换后的数据，并根据目标值对数据点进行着色。我们将轴标记为 PC1 和 PC2，它们分别代表第一和第二主成分，并使用 plt.show() 显示绘图。

输出

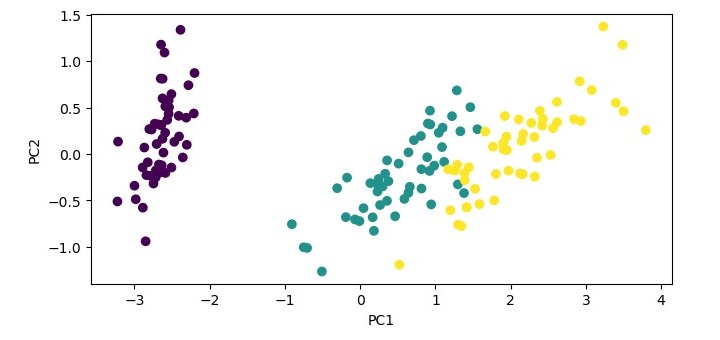
执行给定程序时，它将生成以下绘图作为输出：

特征提取的优势

以下是使用特征提取的优势：

降维 - 特征提取通过将数据转换为一组新的特征来降低输入数据的维度。这使得数据更容易可视化、处理和分析。
性能提升 - 特征提取可以通过创建一组更有意义的特征来提高机器学习算法的性能，这些特征捕获了输入数据中的基本信息。
特征选择 - 特征提取可用于执行特征选择，方法是选择对机器学习模型信息量最大的最相关特征子集。
降噪 - 特征提取还可以帮助减少数据中的噪声，方法是过滤掉不相关的特征或组合相关的特征。

特征提取的缺点

以下是使用特征提取的缺点：

信息丢失 - 特征提取可能导致信息丢失，因为它涉及减少输入数据的维度。转换后的数据可能不包含原始数据中的所有信息，并且在此过程中可能会丢失一些信息。
过拟合 - 如果转换后的特征过于复杂或选择的特征数量过多，特征提取也可能导致过拟合。
复杂度 - 特征提取在计算上可能代价高昂且耗时，尤其是在处理大型数据集或复杂的特征提取技术（如深度学习）时。
领域专业知识 - 特征提取需要领域专业知识才能有效地选择和转换特征。它需要了解数据和手头的问题才能选择对机器学习模型信息量最大的正确特征。

打印页面