机器学习 - 基于分布的聚类

基于分布的聚类算法，也称为概率聚类算法，是一类机器学习算法，假设数据点是由概率分布的混合生成的。这些算法旨在识别生成数据的潜在概率分布，并利用此信息将数据聚类成具有相似属性的组。

一种常见的基于分布的聚类算法是高斯混合模型 (GMM)。GMM假设数据点是由高斯分布的混合生成的，并旨在估计这些分布的参数，包括每个分布的均值和协方差。下面我们来看看什么是ML中的GMM以及如何在Python编程语言中实现它。

高斯混合模型

高斯混合模型 (GMM) 是一种流行的机器学习聚类算法，它假设数据是由高斯分布的混合生成的。换句话说，GMM试图将一组高斯分布拟合到数据中，其中每个高斯分布代表数据中的一个聚类。

与其他聚类算法相比，GMM 具有几个优势，例如能够处理重叠聚类、对数据的协方差结构进行建模以及为每个数据点提供概率聚类分配。这使得 GMM 成为许多应用中的流行选择，例如图像分割、模式识别和异常检测。

Python实现

在 Python 中，Scikit-learn 库提供了 GaussianMixture 类来实现 GMM 算法。该类接受几个参数，包括组件数量（即要识别的聚类数量）、协方差类型和初始化方法。

以下是如何使用 Python 中的 Scikit-learn 库实现 GMM 的示例：

示例

from sklearn.mixture import GaussianMixture
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt

# generate a dataset
X, _ = make_blobs(n_samples=200, centers=4, random_state=0)

# create an instance of the GaussianMixture class
gmm = GaussianMixture(n_components=4)

# fit the model to the dataset
gmm.fit(X)

# predict the cluster labels for the data points
labels = gmm.predict(X)

# print the cluster labels
print("Cluster labels:", labels)
plt.figure(figsize=(7.5, 3.5))
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis')
plt.show()

在此示例中，我们首先使用 Scikit-learn 中的 make_blobs() 函数生成一个合成数据集。然后，我们创建一个具有 4 个组件的 GaussianMixture 类的实例，并使用 fit() 方法将模型拟合到数据集。最后，我们使用 predict() 方法预测数据点的聚类标签，并打印结果标签。

输出

执行此程序时，它将生成以下图表作为输出：

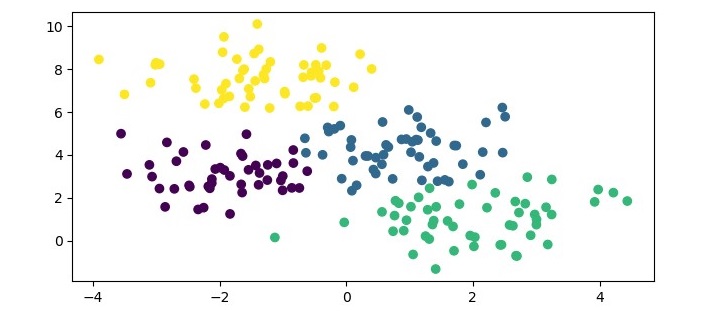
此外，您将在终端上获得以下输出：

Cluster labels: [2 0 1 3 2 1 0 1 1 1 1 2 0 0 2 1 3 3 3 1 3 1 2 0 2 2 3 2 2 1 3 1 0 2 0 1 0
   1 1 3 3 3 3 1 2 0 1 3 3 1 3 0 0 3 2 3 0 2 3 2 3 1 2 1 3 1 2 3 0 0 2 2 1 1
   0 3 0 0 2 2 3 1 2 2 0 1 1 2 0 0 3 3 3 1 1 2 0 3 2 1 3 2 2 3 3 0 1 2 2 1 3
   0 0 2 2 1 2 0 3 1 3 0 1 2 1 0 1 0 2 1 0 2 1 3 3 0 3 3 2 3 2 0 2 2 2 2 1 2
   0 3 3 3 1 0 2 1 3 0 3 2 3 2 2 0 0 3 1 2 2 0 1 1 0 3 3 3 1 3 0 0 1 2 1 2 1
   0 0 3 1 3 2 2 1 3 0 0 0 1 3 1]

GMM 中的协方差类型参数控制用于高斯分布的协方差矩阵的类型。可用选项包括“full”（完整协方差矩阵）、“tied”（所有聚类的绑定协方差矩阵）、“diag”（对角协方差矩阵）和“spherical”（所有维度的一个方差参数）。初始化方法参数控制用于初始化高斯分布参数的方法。

高斯混合模型的优点

以下是使用高斯混合模型的优点：

• 高斯混合模型 (GMM) 可以对任意数据分布进行建模，使其成为一种灵活的聚类算法。

• 它可以处理具有缺失或不完整数据的数据集。

• 它为聚类提供了一个概率框架，可以提供有关聚类结果不确定性的更多信息。

• 它可用于密度估计和生成遵循与原始数据相同分布的新数据点。

• 它可用于半监督学习，其中一些数据点具有已知的标签并用于训练模型。

高斯混合模型的缺点

以下是使用高斯混合模型的一些缺点：

• GMM 对初始参数的选择很敏感，例如聚类数量以及聚类均值和协方差的初始值。

• 对于高维数据集，它在计算上可能很昂贵，因为它涉及计算协方差矩阵的逆，对于大型矩阵来说，这可能很昂贵。

• 它假设数据是由高斯分布的混合生成的，这可能不适用于所有数据集。

• 它可能容易过拟合，尤其是在参数数量很大或数据集很小的情况下。

• 解释结果聚类可能很困难，尤其是在协方差矩阵很复杂的情况下。