Mahotas - Daubechies 小波

---

---

Daubechies 小波是正交小波，指的是可以使用波来表示图像的数学函数。

Daubechies 小波在有限区间内只有非零值，其特征是消失矩的最大数量。

小波的消失矩指的是等于零的矩的数量。矩是小波函数乘以 x 的幂的积分（曲线下的面积）。

具有更多消失矩的小波可以更好地表示平滑信号，而具有较少消失矩的小波可以更好地表示具有不连续性的信号。

Mahotas 中的 Daubechies 小波

在 Mahotas 中，我们可以使用 **mahotas.daubechies()** 函数对图像应用 Daubechies 小波变换。

它支持从 D2 到 D20 的多种 Daubechies 小波，其中整数表示小波中消失矩的数量。

这些变换涉及将图像分解成低频（平滑特征）和高频系数（细节特征）。这使得可以独立分析图像的不同频率。

mahotas.daubechies() 函数

mahotas.daubechies() 函数以灰度图像作为输入，并将小波系数作为新图像返回。

小波系数是一个元组，其中包含对应于图像平滑和细节特征的数组。

语法

以下是 mahotas 中 daubechies() 函数的基本语法：

mahotas.daubechies(f, code, inline=False)

其中，

• **f** - 输入图像。

• **code** - 指定要使用的小波类型，可以是 'D2'、'D4'、……、'D20'。

• **inline (可选)** - 指定是返回新图像还是修改输入图像（默认为 False）。

示例

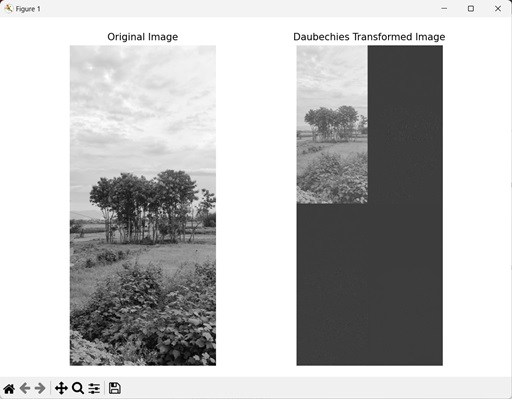
在以下示例中，我们使用 mh.daubechies() 函数对图像应用 Daubechies 小波变换。

import mahotas as mh
import numpy as np
import matplotlib.pyplot as mtplt
# Loading the image
image = mh.imread('nature.jpeg')
# Converting it to grayscale
image = mh.colors.rgb2gray(image)
# Applying Daubechies transformation
daubechies_transform = mh.daubechies(image, 'D20')
# Creating a figure and axes for subplots
fig, axes = mtplt.subplots(1, 2)
# Displaying the original image
axes[0].imshow(image, cmap='gray')
axes[0].set_title('Original Image')
axes[0].set_axis_off()
# Displaying the Daubechies transformed image
axes[1].imshow(daubechies_transform, cmap='gray')
axes[1].set_title('Daubechies Transformed Image')
axes[1].set_axis_off()
# Adjusting spacing between subplots
mtplt.tight_layout()
# Showing the figures
mtplt.show()

输出

以下是上述代码的输出：

多个 Daubechies 小波

另一种应用 Daubechies 小波变换的方法是使用多个 Daubechies 小波。多个 Daubechies 小波指的是一组具有不同消失矩的小波。

在 mahotas 中，要应用多个 Daubechies 小波，我们首先创建一个不同小波的列表。然后，我们遍历列表中的每个小波。

最后，我们使用 mh.daubechies() 函数将不同的小波应用于输入图像。

例如，假设我们有一个包含三个小波的列表：D6、D12 和 D18。这三个小波分别具有 6、12 和 18 个消失矩。

因此，将生成三个输出图像，每个图像都应用了不同的 Daubechies 小波。

示例

在下面提到的示例中，我们对图像应用了多个 Daubechies 小波变换。

import mahotas as mh
import numpy as np
import matplotlib.pyplot as mtplt
# Loading the image
image = mh.imread('sun.png')
# Converting it to grayscale
image = mh.colors.rgb2gray(image)
# Creating list of multiple Daubechies wavelets
daubechies_wavelets = ['D6', 'D12', 'D18']
# Creating subplots to display images for each Daubechies wavelet
fig, axes = mtplt.subplots(1, len(daubechies_wavelets) + 1)
axes[0].imshow(image, cmap='gray')
axes[0].set_title('Original Image')
axes[0].set_axis_off()
# Applying Daubechies transformation for each Daubechies wavelet
for i, daubechies in enumerate(daubechies_wavelets):
   daubechies_transform = mh.daubechies(image, daubechies)
   axes[i + 1].imshow(daubechies_transform, cmap='gray')
   axes[i + 1].set_title(f'Wavelet={daubechies}')
   axes[i + 1].set_axis_off()
# Adjusting spacing between subplots
mtplt.tight_layout()
# Showing the figures
mtplt.show()

输出

上述代码的输出如下：

随机图像上的 Daubechies 小波

我们还可以通过对二维随机图像使用 Daubechies 小波来执行 Daubechies 变换。

二维随机图像指的是每个像素具有随机强度值的图像。强度值可以从 0（黑色）到 255（白色）。

在 mahotas 中，要对随机图像执行 Daubechies 小波变换，我们首先指定 2D 图像的维度（长度和宽度）。

然后，我们将这些维度以及强度范围（0 到 255）传递给 np.random.randint() 函数以创建随机图像。由于未指定通道值，因此创建的图像是灰度图像。

之后，我们通过指定要使用的小波来应用 Daubechies 小波变换。

示例

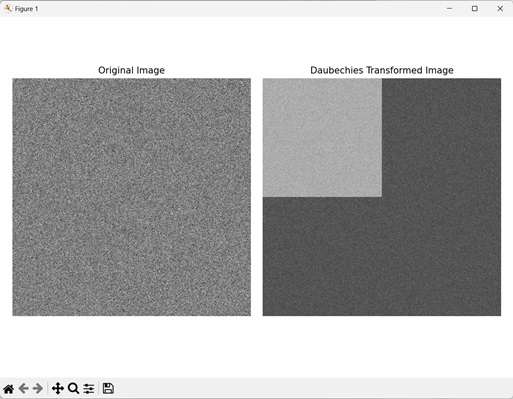
在这里，我们对随机生成的二维图像应用 Daubechies 小波变换。

import mahotas as mh
import numpy as np
import matplotlib.pyplot as mtplt
# Specifying the dimensions
length, width = 1000, 1000
# Creating a random two-dimensional image
image = np.random.randint(0, 256, (length, width))
# Applying Daubechies transformation
daubechies_transform = mh.daubechies(image, 'D2')
# Creating a figure and axes for subplots
fig, axes = mtplt.subplots(1, 2)
# Displaying the original image
axes[0].imshow(image, cmap='gray')
axes[0].set_title('Original Image')
axes[0].set_axis_off()
# Displaying the Daubechies transformed image
axes[1].imshow(daubechies_transform, cmap='gray')
axes[1].set_title('Daubechies Transformed Image')
axes[1].set_axis_off()
# Adjusting spacing between subplots
mtplt.tight_layout()
# Showing the figures
mtplt.show()

输出

执行上述代码后，我们将得到以下输出：