
- Mahotas 教程
- Mahotas - 首页
- Mahotas - 简介
- Mahotas - 计算机视觉
- Mahotas - 历史
- Mahotas - 特性
- Mahotas - 安装
- Mahotas 图像处理
- Mahotas - 图像处理
- Mahotas - 加载图像
- Mahotas - 加载灰度图像
- Mahotas - 显示图像
- Mahotas - 显示图像形状
- Mahotas - 保存图像
- Mahotas - 图像的质心
- Mahotas - 图像卷积
- Mahotas - 创建 RGB 图像
- Mahotas - 图像的欧拉数
- Mahotas - 图像中零值的比例
- Mahotas - 获取图像矩
- Mahotas - 图像中的局部最大值
- Mahotas - 图像椭圆轴
- Mahotas - 图像拉伸 RGB
- Mahotas 颜色空间转换
- Mahotas - 颜色空间转换
- Mahotas - RGB 到灰度转换
- Mahotas - RGB 到 LAB 转换
- Mahotas - RGB 到 Sepia 转换
- Mahotas - RGB 到 XYZ 转换
- Mahotas - XYZ 到 LAB 转换
- Mahotas - XYZ 到 RGB 转换
- Mahotas - 增加伽马校正
- Mahotas - 拉伸伽马校正
- Mahotas 标签图像函数
- Mahotas - 标签图像函数
- Mahotas - 图像标记
- Mahotas - 区域过滤
- Mahotas - 边界像素
- Mahotas - 形态学操作
- Mahotas - 形态学运算符
- Mahotas - 查找图像均值
- Mahotas - 裁剪图像
- Mahotas - 图像的偏心率
- Mahotas - 图像叠加
- Mahotas - 图像的圆度
- Mahotas - 图像缩放
- Mahotas - 图像直方图
- Mahotas - 图像膨胀
- Mahotas - 图像腐蚀
- Mahotas - 分水岭算法
- Mahotas - 图像开运算
- Mahotas - 图像闭运算
- Mahotas - 填充图像中的孔洞
- Mahotas - 条件膨胀图像
- Mahotas - 条件腐蚀图像
- Mahotas - 图像条件分水岭
- Mahotas - 图像中的局部最小值
- Mahotas - 图像的区域最大值
- Mahotas - 图像的区域最小值
- Mahotas - 高级概念
- Mahotas - 图像阈值化
- Mahotas - 设置阈值
- Mahotas - 软阈值
- Mahotas - Bernsen 局部阈值化
- Mahotas - 小波变换
- 制作图像小波中心
- Mahotas - 距离变换
- Mahotas - 多边形实用程序
- Mahotas - 局部二值模式
- 阈值邻域统计
- Mahotas - Haralick 特征
- 标记区域的权重
- Mahotas - Zernike 特征
- Mahotas - Zernike 矩
- Mahotas - 排序滤波器
- Mahotas - 2D 拉普拉斯滤波器
- Mahotas - 多数滤波器
- Mahotas - 均值滤波器
- Mahotas - 中值滤波器
- Mahotas - Otsu 方法
- Mahotas - 高斯滤波
- Mahotas - 击中击不中变换
- Mahotas - 标记最大数组
- Mahotas - 图像的平均值
- Mahotas - SURF 密集点
- Mahotas - SURF 积分
- Mahotas - Haar 变换
- 突出显示图像最大值
- 计算线性二值模式
- 获取标签的边界
- 反转 Haar 变换
- Riddler-Calvard 方法
- 标记区域的大小
- Mahotas - 模板匹配
- 加速鲁棒特征
- 去除边界标记
- Mahotas - Daubechies 小波
- Mahotas - Sobel 边缘检测
Mahotas - 形态学运算符
形态学运算符是一组图像处理技术,有助于修改图像中物体的形状、大小和空间关系。它们就像用于重塑或操纵图像中物体的工具。
想象一下,您有一张包含各种物体(如圆形、正方形和线条)的图片。形态学运算符允许您以不同的方式更改这些物体的外观。
例如,您可以使它们更大或更小、平滑其边缘、去除微小细节或填充间隙。
为了实现这些转换,形态学运算符使用数学运算,这些运算涉及使用称为结构元素的特殊模式扫描图像。此结构元素定义了在操作期间将考虑的每个像素周围邻域的形状和大小。
Mahotas 和形态学运算符
Mahotas 提供了一套全面的形态学运算符,可应用于二值、灰度或多通道图像。这些运算符使用优化的算法高效地实现,使其适用于具有大规模数据集的实际应用。
让我们看看在 mahotas 中可以执行的一些形态学操作:
膨胀
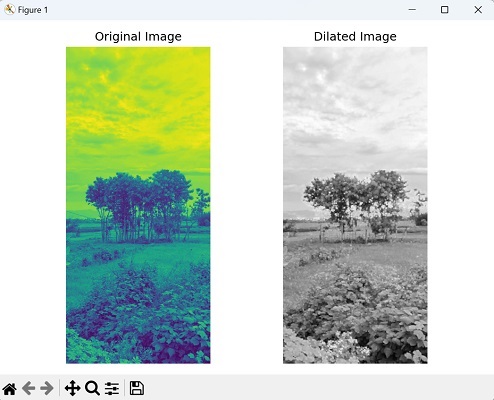
膨胀是一种形态学运算,它扩展图像中物体边界上的像素。它涉及使用结构元素扫描图像,并用结构元素定义的相应邻域内的最大值替换每个像素。
让我们看看下面原始图像以及膨胀后的图像:
腐蚀
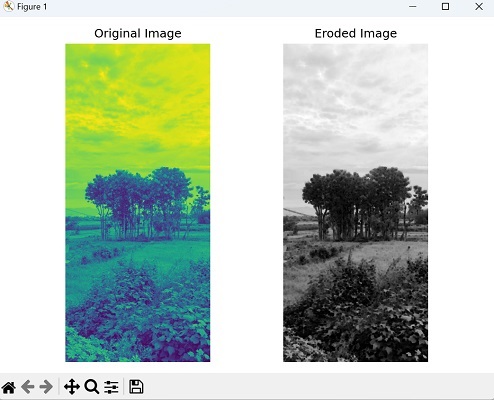
腐蚀是一种基本的形态学运算符,它会收缩或腐蚀图像中物体边界上的像素。
以下是腐蚀后的图像及其原始图像:
开运算
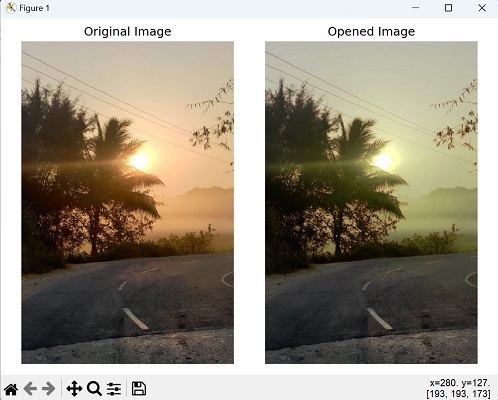
开运算是先腐蚀后膨胀的组合。它去除小物体并填充前景中的小孔,同时保留较大物体的整体形状和连通性。
让我们看看在 mahotas 中的开运算后的图像:
闭运算
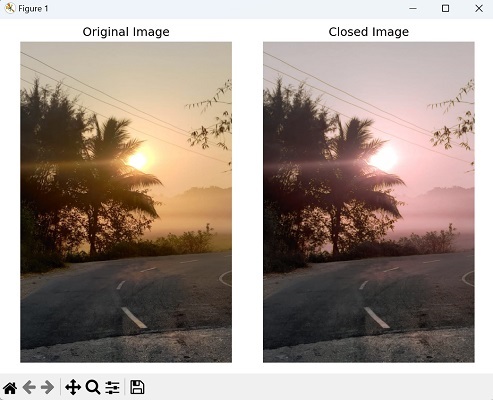
闭运算是开运算的反向操作,包括先膨胀后腐蚀。它填充前景中的小间隙和孔洞,确保物体的连通性。
现在,让我们看看在 mahotas 中的闭运算后的图像:
条件腐蚀
条件腐蚀是一种形态学运算,它根据用户定义的条件保留图像中的结构。它根据称为标记图像的第二幅图像指定的条件选择性地腐蚀图像区域。
该运算仅在标记图像具有非零值的地方腐蚀图像。
下图显示了条件腐蚀:

条件膨胀
条件膨胀类似于条件腐蚀,但操作方式相反。它根据标记图像指定的条件选择性地膨胀图像区域。
该运算仅在标记图像具有非零值的地方膨胀图像。
下图显示了条件膨胀:

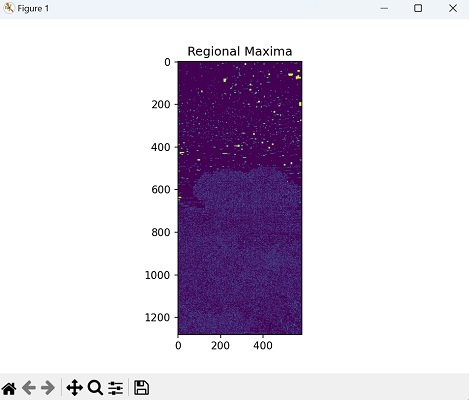
区域最大值
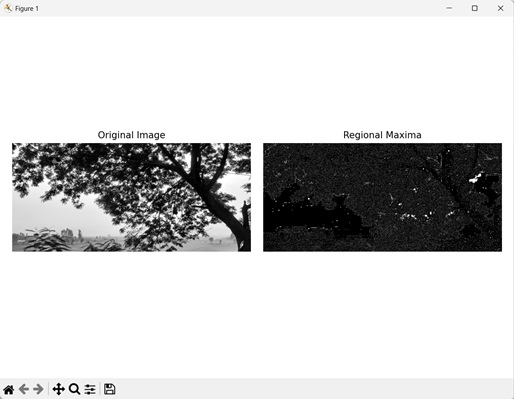
区域最大值是图像中在其邻域内具有最高强度的点。它们代表图像中的局部峰值或显着特征。
Mahotas 中的区域最大值运算符识别这些局部最大值,并将它们标记为前景像素。
下图表示区域最大值:
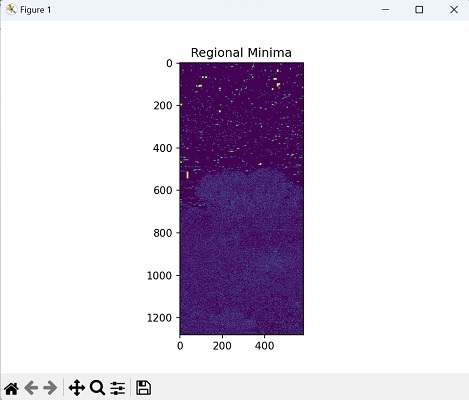
区域最小值
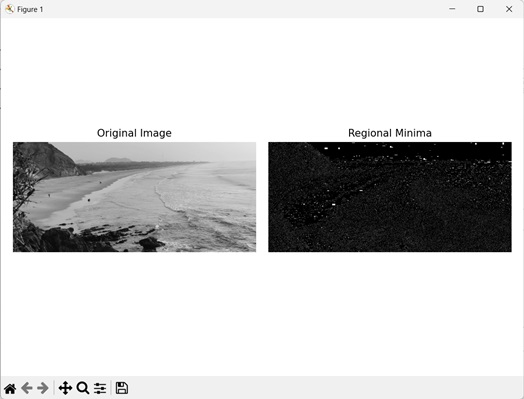
区域最小值是图像中在其邻域内具有最低强度的点。它们代表图像中的局部盆地或凹陷。
Mahotas 中的区域最小值运算符识别这些局部最小值,并将它们标记为背景像素。
下图表示区域最小值:
示例
在以下示例中,我们尝试执行所有上述解释的形态学运算:
import mahotas as mh
import matplotlib.pyplot as plt
import numpy as np
image = mh.imread('nature.jpeg', as_grey=True).astype(np.uint8)
# Dilation
dilated_image = mh.dilate(image, Bc=mh.disk(8))
plt.title("Dilated Image")
plt.imshow(dilated_image)
plt.show()
# Erosion
plt.title("Eroded Image")
eroded_image = mh.erode(image, Bc=mh.disk(8))
plt.imshow(eroded_image)
plt.show()
# Opening
plt.title("Opened Image")
opened_image = mh.open(image)
plt.imshow(opened_image)
plt.show()
# Closing
plt.title("Closed Image")
closed_image = mh.close(image)
plt.imshow(closed_image)
plt.show()
# Conditional Dilation
plt.title("Conditional Dilation")
g = image * 6
cdilated_image = mh.cdilate(image, g)
plt.imshow(cdilated_image)
plt.show()
# Conditional Erosion
plt.title("Conditional Erosion")
scaled_image = image * 0.5
scaled_image = scaled_image.astype(np.uint8)
ceroded_image = mh.cerode(image, scaled_image)
plt.imshow(ceroded_image)
plt.show()
# Regional Maxima
plt.title("Regional Maxima")
regional_maxima = mh.regmax(image)
plt.imshow(regional_maxima)
plt.show()
# Regional Minima
plt.title("Regional Minima")
regional_minima = mh.regmin(image)
plt.imshow(regional_minima)
plt.show()
输出
获得的输出如下所示:
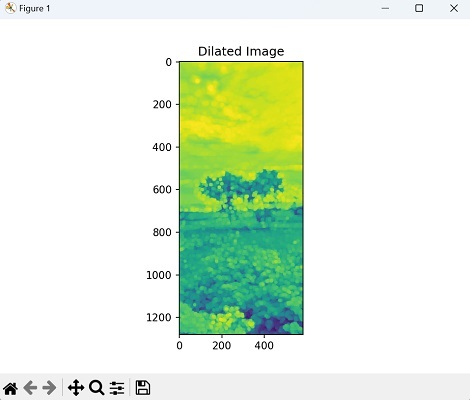
膨胀
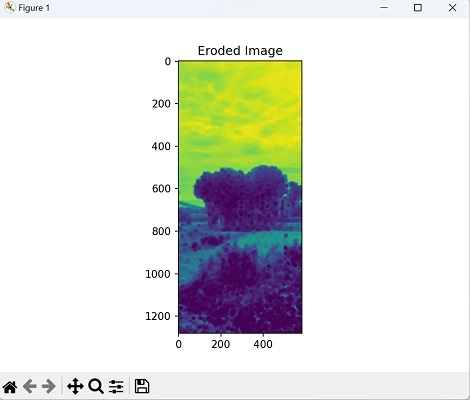
腐蚀
开运算后的图像
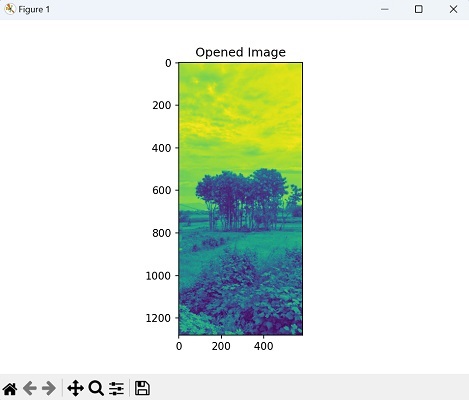
闭运算后的图像
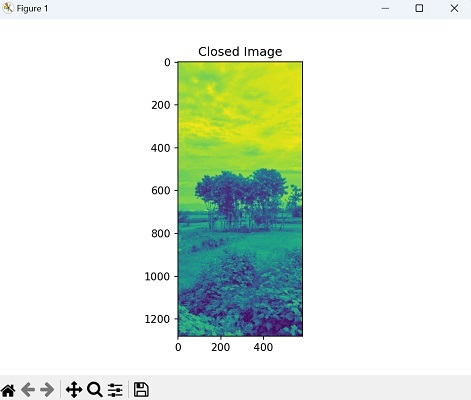
条件膨胀
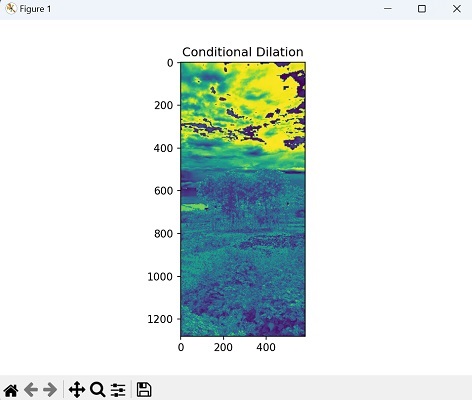
条件腐蚀
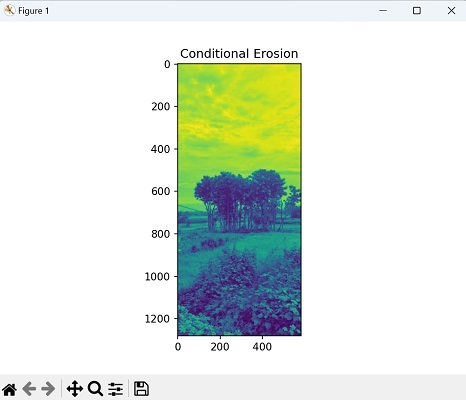
区域最大值
区域最小值
我们将在本节的其余章节中详细讨论所有形态学运算符。