Mahotas - 小波变换

---

---

小波变换是一种将图像分解成不同频率分量的数学技术。小波变换可以捕捉图像的局部和全局细节。

小波变换使用称为小波的小波形函数来分析信号。这些小波经过缩放和平移以匹配图像中存在的不同模式。

小波变换涉及修改频率分量的低频和高频系数，以识别模式并增强图像。可以通过小波逆变换恢复原始图像。

让我们讨论一下小波变换技术及其逆变换。

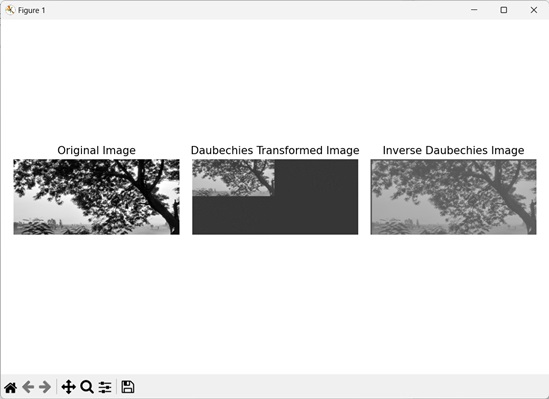
Daubechies变换

Daubechies变换是一种用于将信号分解成不同频率分量的小波变换技术。它允许我们同时在时域和频域分析信号。

让我们看看下面的Daubechies变换图像：

Daubechies逆变换

Daubechies逆变换是Daubechies变换的逆过程。它从通过Daubechies变换获得的各个频率分量重建原始图像。

通过应用逆变换，我们可以恢复信号，同时保留重要的细节。

在这里，我们来看一下Daubechies逆变换：

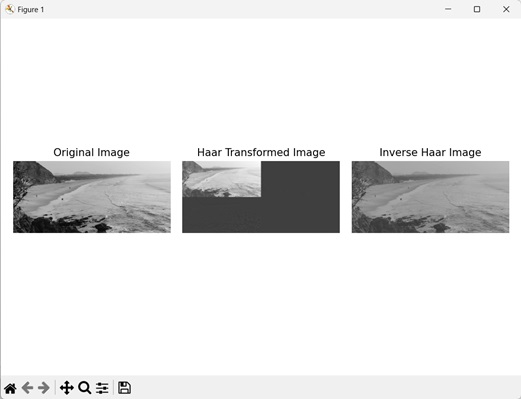
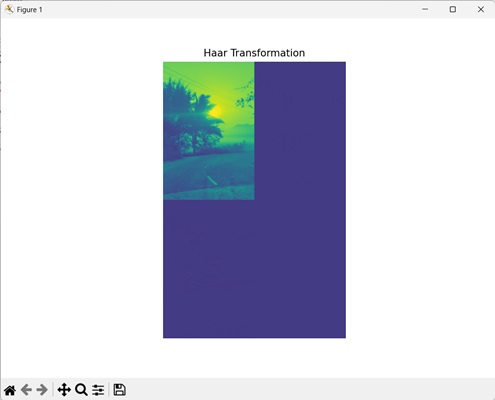
Haar变换

Haar变换技术通过将图像划分成子区域来将其分解成不同的频率分量。然后计算平均值之间的差异，以对图像应用小波变换。

在下图中，我们看到了Haar变换后的图像：

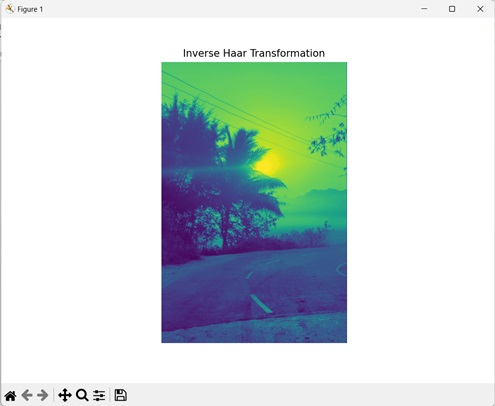
Haar逆变换

Haar逆变换从通过Haar变换获得的频率分量重建原始图像。它是Haar变换的逆运算。

让我们看一下Haar逆变换：

示例

在下面的示例中，我们尝试执行上面解释的所有小波变换：

import mahotas as mh
import numpy as np
import matplotlib.pyplot as mtplt
image = mh.imread('sun.png', as_grey=True)
# Daubechies transformation
daubechies = mh.daubechies(image, 'D6')
mtplt.imshow(daubechies)
mtplt.title('Daubechies Transformation')
mtplt.axis('off')
mtplt.show()
# Inverse Daubechies transformation
daubechies = mh.daubechies(image, 'D6')
inverse_daubechies = mh.idaubechies(daubechies, 'D6')
mtplt.imshow(inverse_daubechies)
mtplt.title('Inverse Daubechies Transformation')
mtplt.axis('off')
mtplt.show()
# Haar transformation
haar = mh.haar(image)
mtplt.imshow(haar)
mtplt.title('Haar Transformation')
mtplt.axis('off')
mtplt.show()
# Inverse Haar transformation
haar = mh.haar(image)
inverse_haar = mh.ihaar(haar)
mtplt.imshow(inverse_haar)
mtplt.title('Inverse Haar Transformation')
mtplt.axis('off')
mtplt.show()

输出

获得的输出如下所示：

Daubechies变换

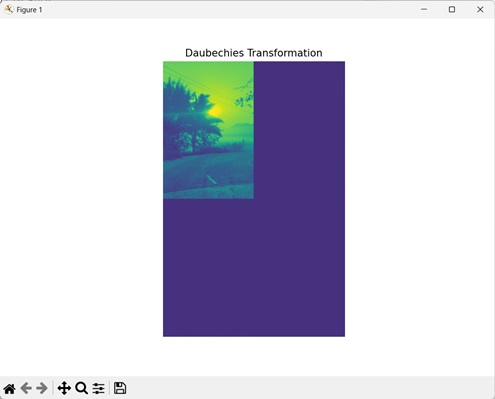
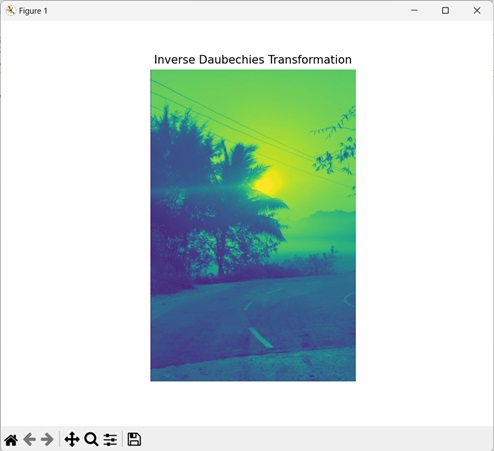
Daubechies逆变换

Haar变换

Haar逆变换

我们将在后面的章节中详细讨论所有的小波变换。