推理 - 时钟
时钟的时针和分针之间可以形成最大180o的角度。当发生这种情况时,两只指针都表示一条直线。
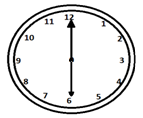
时钟的时针和分针每小时形成两次直角,当它们相隔15分钟时。
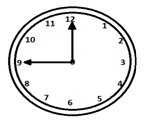
时钟的两根指针每小时重合一次。
时钟对于每个人安排日常任务都非常重要。时钟理论与日常生活相关。
时钟是一种通过将时间划分为小时、分钟和秒来显示时间的仪器。
表盘
它有一个从1到12的圆形表盘,表示小时。表盘的圆周进一步细分为60个相等的空间,这些空间称为分钟空间。
1小时 = 60分钟
1分钟 = 60秒,并且
1小时 = 3600秒
技巧
在n点到(n+1)点之间,时钟的两根指针将在n点后$\left ( \frac{60n}{11} \right )$分钟重合。
在n点到(n+1)点之间,时钟的两根指针将在n点后$\left ( 5n \pm 15 \right )\times\frac{12}{11}$分钟互相形成直角。
在n点到(n+1)点之间,时钟的两根指针将在n点后成一直线(不在一起)
$\left ( 5n - 30 \right )\times\frac{12}{11}$分钟,(当n >6时)
$\left ( 5n + 30 \right )\times\frac{12}{11}$分钟,(当n <6时)
在n点到(n+1)点之间,时钟的两根指针相隔x分钟,在n点后$\left ( 5n \pm x \right )\times\frac{12}{11}$分钟。‘+’号表示分针领先,‘–’号表示时针领先。
如果时钟的分针以x分钟的正确时间间隔追上时针,则时钟损失或获得$\left ( \frac{720}{11} - x \right )\left ( \frac{60 \times 24}{x} \right )$分钟。
1 − 在7点15分到8点15分之间,时钟的时针和分针将在何时重合?
选项 −
A - $39\frac{5}{11}$
B - $39\frac{4}{11}$
C - $38\frac{5}{11}$
D - $39\frac{4}{11}$
答案 − A
解释 −
$\frac{60 \times n}{11} = \frac{60}{11} \times \frac{29}{4} = 39\frac{5}{11}$
其中$n = 7.15 = 7\frac{15}{60} = \frac{29}{4}$
2 − 在9点到8点之间,在什么特定时间,两根指针将成直角?
选项 −
A - 9点后$65\frac{4}{11}$和$32\frac{7}{11}$分钟
B - 9点后$65\frac{2}{11}$和$32\frac{2}{11}$分钟
C - 9点后$65\frac{3}{11}$和$32\frac{3}{11}$分钟
D - 9点后$65\frac{1}{11}$和$32\frac{1}{11}$分钟
答案 − A
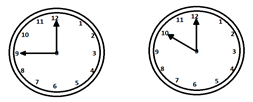
解释 −
$\left ( 5n \pm 15 \right ) \times\frac{12}{11} = \left ( 5\times9\pm 15 \right )\times\frac{12}{11}$
$= 65\frac{4}{11}$和$32\frac{7}{11}$分钟,9点后
3 − 在12点到1点之间,时钟的两根指针将在何时形成一条直线?
选项 −
A - 12点后$\frac{360}{11}$分钟。
B - 12点后$\frac{355}{11}$分钟。
C - 12点后$\frac{340}{11}$分钟。
D - 12点后$\frac{345}{11}$分钟。
答案 − D
解释 −
$\left ( 5n-30 \right )\times\frac{12}{11}$分钟,12点后
$\left ( 6-30 \right )\times\frac{12}{11}$分钟,12点后
$= \frac{345}{11}$分钟,12点后(因为n = 12)
4 − 时钟的指针将在何时相隔30分钟的空间,当它们在星期一12点到下午1点之间?
选项 −
A - 12点后$\frac{1080}{11}$和$\frac{300}{11}$分钟
B - 12点后$\frac{1080}{12}$和$\frac{360}{11}$分钟
C - 12点后$\frac{1080}{11}$和$\frac{360}{11}$分钟
D - 12点后$\frac{1080}{12}$和$\frac{300}{12}$分钟
答案 − C
解释 −
$\left ( 5n\pm x \right )\times\frac{12}{11}$
$= \left ( 5\times12\pm 30 \right )\times\frac{12}{11}$
$= \frac{90\times12}{11}$和$\frac{30\times12}{11}$分钟,12点后 = $\frac{1080}{11}$和$\frac{360}{11}$分钟,12点后
5 − 时钟的分针以61分钟的间隔追上时针,则时钟损失或获得多少时间?
选项 −
A - $104\frac{4}{671}$分钟。
B - $105\frac{1}{671}$分钟。
C - $104\frac{3}{671}$分钟。
D - $105\frac{4}{671}$分钟。
答案 − B
解释 −
$\left ( \frac{720}{11}-61 \right )\times\left ( \frac{60\times24}{61} \right )$
$= 105\frac{1}{671}$分钟。
