推理 - 缺失字符

插入缺失图形问题通常出现在各种竞争性考试中，主要由一个分成多个区域的图形组成。在这些区域之间，会有数字、字母，或者可能是字母和数字的组合，遵循一定的序列。它们在给定图形内以序列的形式排列。问题可能包含单个图形或两个或两个以上图形的组合。问题图形可以是任何几何图形，例如矩形、三角形、圆形或任何其他类型的非典型图形，其中包含一组数字或字母。图形可以根据问题背后的逻辑和序列分成许多部分。在问题图形中，给定的数字或字母将在每个步骤中发生变化，遵循一定的序列或逻辑。读者需要分析序列或数字或逻辑，并从给定的选项中选择正确的答案。

在这种类型的题目中，会给出一个包含字母或数字的单个图形，这些字母或数字遵循一定的序列或逻辑，如下面的例子所示。

示例 1

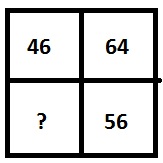
选项 −

A − 83

B − 54

C − 65

D − 60

答案 − 选项 C

解释 − 在此示例中，问题图形内部有四个区域，其中包含一些数字，这些数字在下一步中交换位置，因此 56 可以写成 65 来替换问号。

这种类型的题目可能包含一个分成多个部分的图形，其中包含数字或字母，如下所示：

等等。

示例 2

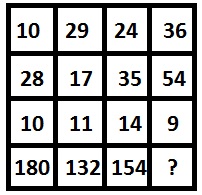
选项 −

A − 150

B − 145

C − 165

D − 162

答案 − 选项 D

解释 − 底行的数字是通过 (28 - 10) × 10 = 180、(29 - 17) × 11 = 132、(3524) × 14 = 154 获得的，因此缺失的数字是 (54 - 36) × 9 = 162。

在这种类型的图形中，问题将包含两个或两个以上图形，其中第一个或两个图形提供了关于问题序列或逻辑的信息，读者需要分析它们并选择正确的答案，如下面的例子所示。

示例 3

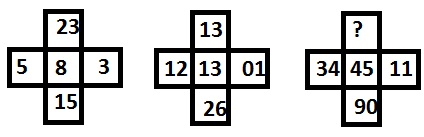
选项 −

A − 36

B − 40

C − 45

D − 以上均不正确

答案 − 选项 C

解释 − 在上图中，数字之间的关系是从第一个和第二个图形得出的，即 5 + 3 = 8 = 2315，类似地，答案可以求得为 34 + 11 = 45 = 90 - 45。因此，缺失的数字是 45。