推理 - 三段论
希腊人给出的三段论的含义是演绎。这是一种逻辑论证。
一些重要术语的定义
下面给出一些术语,这些术语在解决三段论问题中起着重要作用。
命题 - 命题是一个陈述句。命题由三部分组成:a) 主语,b) 谓语,c) 主语和谓语之间的关系。下面给出一些命题。
- 所有海岸都是海滩。
- 没有学生是诚实的。
- 有些文件是秘密的。
主语和谓语 - 主语是被叙述的对象。另一方面,谓语是与主语相关的部分。例如 - 从上面的命题中,海岸、学生、文件是主语,而海滩、诚实和秘密是谓语。
范畴命题的类型
全称命题 - 全称命题是指完全包含或完全排除主语的命题。例如 - 没有学生是聪明的。全称命题进一步分为以下几类 -
全称肯定命题 - 当形式为所有 X 都是 Y时,称为肯定命题。通常用字母A表示。
全称否定命题 - 当形式为没有 X 是 T时,称为否定命题。用E表示。
特称命题 - 它是部分显示或部分排除主语但不完全排除主语的命题。例如,有些猫是棉花。它也分为以下类型 -
特称肯定命题 - 像有些 X 是 U这样的形式称为特称肯定命题。它们编码为I。
特称否定命题 - 像有些 T 不是 P这样的形式,例如有些猫不是线圈,称为特称否定命题,编码为O。
间接推理 - 结论是从两个语句中得出的。例如 - “所有嘴唇都是线圈”和“所有球都是球棒”。所以结论将是“所有嘴唇都是线圈”。
直接推理 - 结论将仅从一个命题中得出。例如,如果陈述是“所有老师都是神”,那么结论将是“有些老师是神”。
直接推理的两种重要方法
这些方法包括转换、反对等。
蕴含 - 假设给定“所有猫都是海滩”,那么它表明结论“有些猫是海滩”是正确的。因此,如果给定的命题属于 A 类,那么它也表明 I 类结论必须为真。
转换 - 它包括两个步骤。
步骤 1 - 主语将转换为谓语,反之亦然。
步骤 2 - 给定的命题将相应地改变。
例如 -
陈述 - 所有猫都是架子。所有包都是架子。有些钱包是包。
结论 -
1. 有些猫是包。
2. 有些架子是猫。
3. 有些架子是钱包。
A - 只有 1
B - 只有 2 和 3
C - 只有 1 和 2
D - 只有 1 和 3
解答 -
答案 - B 选项
欧拉提出了表示命题的图解方法。根据四个命题,关系可以有四种表达方式。
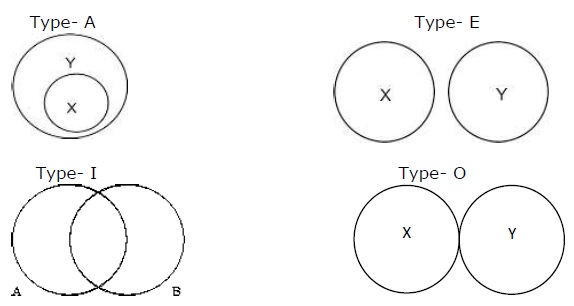
类型 - A 代表“所有 X 都是 Y”,类型 - E 代表“没有 X 是 Y”,类型 - I 代表“有些 A 是 B”,类型 - O 代表“有些 X 不是 Y”。
例如 -
陈述 -有些相机是笔记本电脑。
有些笔记本电脑是手机。
有些手机是平板电脑。
结论 -
I - 至少有些平板电脑是相机
II - 所有平板电脑都是笔记本电脑是有可能的
III - 没有平板电脑是笔记本电脑
解答 -
圆形图 -
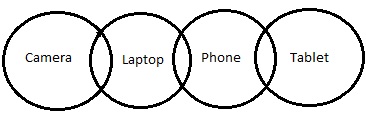
根据上图,
结论 III 成立。但是陈述中提到了“可能性”这个词。所以让我们检查一下可能性。
新的图表将是 -
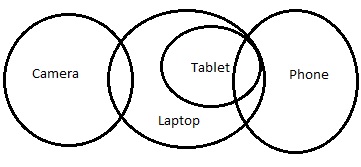
但在这种情况下,结论 III 不成立。结论 II 或结论 III 之一成立。
