推理 - 图形系列

图形系列问题通常在竞争性考试中被用来测试考生的推理能力。它需要考生能够快速做出决策、快速解决问题的能力、良好的比较能力以及快速找到各种问题背后原因的能力。它测试考生快速想象和找到正确解决方案的能力。问题中的图形可能包含各种几何图形、数字、符号或其他图片。图形系列问题可能有多种类型。

提出的各种类型的问题包括：

示例-1

在处理这些类型的图形时，考生必须找出每个图形依次变化的序列，或者必须找出它们之间相互的关系。

例如，让我们找出将继续下面给出的序列的图形。

示例 - 找到将继续图形序列的图形？

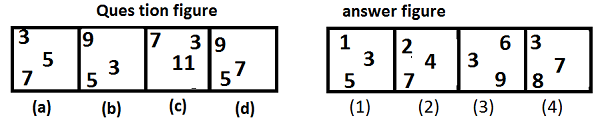
答案 - 图形 (1)

解释 -

从上图可以清楚地看出，问题图形在每个框中包含一组不同的数字，这些数字都是奇数。

示例-2

可能会要求考生从给定的选项中选择正确的图形，以替换问题图形上的问号。这些类型的问题通常包含一系列图形，这些图形根据一定的顺序改变其形状、外观或位置。考生必须比较给定的图形并找出图形的顺序，然后从给定的选项中选择符合顺序的正确图形。以下面的例子可以更清楚地说明这一点。

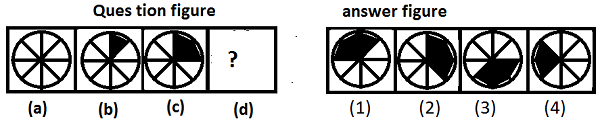
示例 - 找出将替换问号的图形。

答案 - 选项 (2)

解释 -

该序列的顺序是圆被分成多个扇形，每次添加一条弦，并按顺时针方向进行阴影。

示例-3

有时会给出两个相关的图形，并且会要求考生从给定的选项中找出与第三个图形顺序相关的图形。考生必须了解前两个图形的顺序（它们之间是如何相关的），并选择一个与第三个图形相关的选项，其方式与前一对图形相同。下面的示例将更清楚地说明这一点。

示例 - 哪个图形可以放在问号的位置？

答案 - 选项 (2)

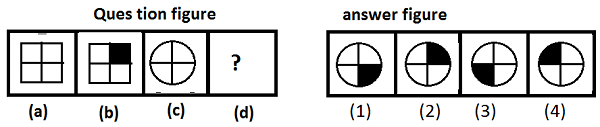
解释 - 图形 (a) 和 (b) 通过对右上角四分之一部分进行阴影而相互关联，因此，图形 (2) 将与图形 (c) 形成对。

示例-4

可能会给出一些问题，这些问题包含一个核心图形，并且会根据一定的顺序在每个步骤中发生变化。会要求考生找出与其他图形不同的图形，即违反序列顺序的图形。

示例 - 找出下面图形中与其他图形不同的图形。

答案 - 图形 (4)

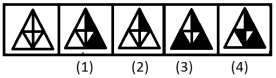
解释 - 在每个步骤中，主图形的两个空格被阴影覆盖，并在下一步中擦除一个空格，此序列在整个系列中重复，根据此序列，第四个图形必须有两个阴影图形，但事实并非如此，因此它是答案图形。

示例-5

有时会给出一系列类似的图形，并且会要求考生从给定的选项中找出与问题图形类似的图形，如下面的例子所示。

示例 - 找出与问题图形类似的图形。

答案 - 图形 (3)

解释 - 在问题图形中，所有块都包含两个相互接触的图形，并且其中任何一个图形的一半都被阴影覆盖。问题图形中的序列还显示，在奇数块中，顶部图形为空，底部图形被阴影覆盖，而在偶数块中，顶部图形被阴影覆盖，而底部图形为空。因此，图形 (3) 与问题图形相同。