推理 - 编码二进制数

底数为 2 的数称为二进制数。二进制数由 0 和 1 的补码组成。因此，编码二进制数包含两个过程。一个是二进制转换为十进制，另一个是十进制转换为二进制。

十进制数

要了解什么是二进制数，首先我们必须了解十进制数。因此，十进制数由十个数字组成（即 0、1、2、3、4、5、6、7、8、9）。任何十进制系统都可以用这些数字表示。例如，一个数字序列是 2、4、6 和 8。我们以以下方式进行操作：

2468 = 2 × 10³ + 4 × 10² + 6 × 10¹ + 8 × 10⁰

= 2468

注意 - 在这种情况下，我们通过将序列的不同数字乘以 10 的幂并相加来获得数字的值。这里的 10 称为基数或基。因此，在十进制系统下，我们的基数是 10。

二进制数

我们使用十个数字来表示十进制数；就像我们只使用两个数字来表示二进制数一样。任何数字都可以使用这两个数字表示，即 0 和 1。

二进制数的示例是 - 1101。这里数字序列中存在 4 个数字 - 1、1、0、1。我们以以下方式获得值。

1101 = 1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰

= 8 + 4 + 0 + 1 = 13

因此，二进制数在十进制系统中表示十三。可以通过将序列的不同数字乘以 2 的幂并相加来确定该值。

常规方法 - 在上面的示例中，我们看到要获得任何二进制数的值，我们使用以下规则：

最右边的第一个数字乘以 2⁰ = 1

最右边的第二个数字乘以 2¹ = 2

最右边的第三个数字乘以 2² = 4

类似地，最右边的第 n 个数字乘以 2ⁿ⁻¹

最后，将所有这些相加。

例如 - 将以下二进制数转换为十进制数。

A - 1010

B - 1111

C - 100

D - 10000

解答 -

A - 1010 = 1 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2⁰

B - 1111 = 1 × 2³ + 1 × 2² + 1 × 2¹ + 1 × 2⁰

C - 100 = 1 × 2² + 0 × 2¹ + 0 × 2⁰

D - 10000 = 1 × 2⁴ + 0 × 2³ + 0 × 2² + 0 × 2¹ + 0 × 2⁰

更快捷的方法

步骤一 - 从给定数字的最右边的数字开始，在每个数字下方写 1、2、4、8、16、32……依此类推，当您向左移动时。

步骤二 - 忽略 0 下方的数字。将 1 下方的所有数字相加。

让我们用这种方法解决示例 1。

A - 1010

我们将使用 1、2、4、8，因为这里存在 4 个数字。

我们得到，

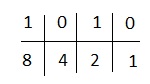
4 和 1 位于零的下方。我们忽略它们并添加其余的。我们得到 8 + 2 = 10

像这样我们可以解决其他数字。

十进制数可以通过连续除法的方法转换为二进制。每次除法时，被除数都除以 2。记录余数，商成为下一个被除数，再次除以 2。重复此过程，直到不再可能进行除法。

例如 - 将 17 转换为二进制数 -

将 17 除以 2，直到不再可能进行除法。

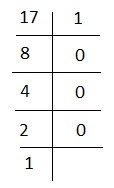
因此，17 的二进制形式为 10001。

方向 (问题 1-4) - 研究以下问题并给出答案。

在某种代码中，0 的符号为 +，1 的符号为 #。没有数字或符号大于 1。1 的符号的值每次向左移动一位时都会加倍。

‘0’ 表示为 +

‘1’ 表示为 #

‘2’ 表示为 #+

‘3’ 表示为 ##

‘4’ 表示为 #++，依此类推

1 - 以下哪个表示 11？

选项 -

A - #+##

B - +##+

C - ##++

D - #+#++

E - 以上皆非

答案 - 选项 A

解释 - 要获得 11 的等价物，我们使用连续除以 2 的方法。

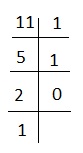
因此二进制形式将为 10111。将 1 和 0 替换为 # 和 +，我们将得到 #+##。

2 - 以下哪个表示 8？

选项 -

A - ##++

B - +##+

C - ##++

D - ++##

E - 以上皆非

答案 - 选项 E

解释 - 对于 8，我们有 -

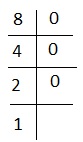
即 1000 或 #+++。正确选择是 5。

3 - 以下哪个将由 ##+# 表示？

选项 -

A - 8

B - 11

C - 13

D - 12

E - 以上皆非

答案 - 选项 E

解释 - ##+# = 1101 = 1 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰ = 15

4 - 以下哪个数字将由 #+++# 表示？

选项 -

A - 22

B - 31

C - 14

D - 17

E - 以上皆非

答案 - 选项 D

解释 - # + + + # = 10001

= 1 × 2⁴ + 0 × 2³ + 0 × 2² + 0 × 2¹ + 1 × 2⁰

= 16 + 1 = 17

二进制系统以 2 为基数，十进制系统以 10 为基数，三进制系统以 3 为基数，而八进制系统以 8 为基数。在三进制的情况下，我们有三个数字来表示数字。这些是 0、1 和 2。在这种情况下，数字将通过乘以 3 的适当幂来转换为十进制。

例如 -

(12012)₃ = 1 × 3⁴ + 2 × 3³ + 0 × 3² + 1 × 3¹ + 2 × 3⁰ = (104)₃