推理 - 逻辑韦恩图
这是一种通过各种几何结构以图解方式展示2-3个类别之间复杂关系的过程。两个几何结构之间的交集表示它们有一些共同点,而完全隔离则表示相反的情况。虽然从上面看,理论似乎很复杂,但对各种类型示例案例的基本理解将有助于更容易地解决后续问题。
了解韦恩图的各种可能情况,以及何时适用。在三列中,第一列显示韦恩图的类型,第二列用于描述,第三列提供一个示例,以清楚地说明描述。
| 韦恩图 | 适用案例 | 示例 |
|---|---|---|
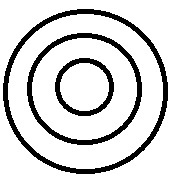 |
将有一系列一个接一个的子案例。 |
颜色>绿色>浅绿色。浅绿色是绿色的一个子部分,两者都属于颜色组。 |
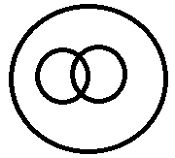 |
一个主类别,在其下有两个子类别,并且两者之间存在一些相似之处。 |
液体>汽油,柴油。这里两者都具有易燃性,因此具有相似性。 |
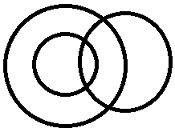 |
一个类别可能有一个子类别。它们都部分满足某些条件(并非总是如此)。 |
蔬菜>辣椒>红色。一些辣椒是红色的,就像一些其他蔬菜一样。 |
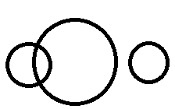 |
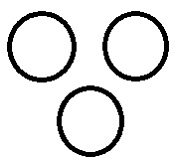
在三个不同的部分中,两个可能具有一些共同的属性,这些属性与第三个部分不匹配。 |
演员>校长>女王。从上面可以看出,演员和校长都表现出男性特征,因此具有一些共同的属性,这与女王正好相反。 |
 |
三个部分没有共同特征。 |
树>愤怒>咖啡。在上述三个术语中找不到任何共同方面的逻辑。 |
 |
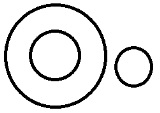
有可能找到一个满足三个单独部分所有属性的共同点。 |
母亲>继母>嫂子。一个女人可以同时是上述所有角色。 |
 |
这尤其适用于以下情况:在三个部分中,两个部分之间存在亲子关系,而第三个部分与它们无关。 |
树>香蕉树>愤怒。我们都知道香蕉树属于树类,但“愤怒”的情绪与这两个词无关。 |
本章中经常出现的另一种类型的题目是各种几何结构的交集。每个几何结构都将拥有自己的一些元素,并且每个结构都将具有一些特征或类别。两个或多个结构的交集将产生一个混合体,这将通过一些新的东西改变每个先前元素的属性。我们必须识别这一点,并需要根据给定的选项做出相应的回答。
五个人被编号并具有一些特征。研究图表以正确回答。
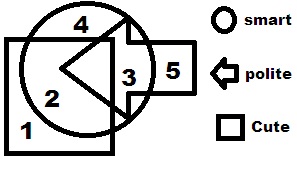
1 - 哪个编号的人聪明又可爱?
A - 1
B - 2
C - 3
D - 4
答案 - B 选项
解释 - 数字 2 位于正方形和圆形的公共区域,因此具有两个结构的特征。
2 - 哪个编号的人聪明但既不礼貌也不可爱?
A - 1
B - 2
C - 3
D - 4
答案 - D 选项
解释 - 数字 4 位于圆形区域,因此只具有聪明的特征。
3 - 哪个编号的人聪明、礼貌且可爱?
A - 1
B - 2
C - 3
D - 以上均不符
答案 - D 选项
解释 - 没有这样的数字位于所有三个几何结构的交集区域。
