推理 - 逻辑推演
逻辑推演是一个重要的章节,因为各种竞争性考试中都包含了许多来自该章节的简单且得分高的题目。在本节中,我们将讨论两种解决此类问题的方法:
- 三段论方法
- 韦恩图方法
基础
如果有两个陈述,那么三段论将是解决问题的最佳方法,但如果陈述的数量超过两个,则使用韦恩图方法。有时,陈述和结论源于普遍接受的事实,但它们也可能是不合逻辑的。例如:
a) 一些椅子是门。
b) 所有男人都是女人
c) 没有牛奶是白色的
得出结论需要抽象思维。需要理解句子的逻辑含义,然后根据逻辑含义回答结论。每个陈述都需要被认为是真实的,然后我们必须验证结论是否在逻辑上遵循陈述。
限定词
这些是一些用来描述一样东西与另一样东西有多相似或不同的基本词汇。一些限定词的例子包括“所有”、“一些”、“一些不”等。
韦恩图概念
另一方面,韦恩图是一种方法,我们可以用几何图形的形式表示句子或陈述。所有给定的陈述都绘制在可能的韦恩图中。然后用这些图验证所有结论。任何满足所有韦恩图的结论都将被视为有效结论。
| 陈述 | 对应的韦恩图 |
|---|---|
| 所有 A 都是 B | 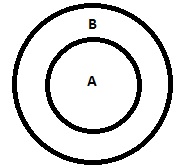 |
| 一些 A 是 B(或)一些 A 不是 B | 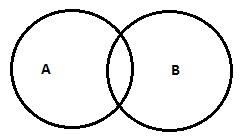 |
| 没有 A 是 B | 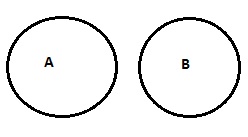 |
让我们举一个简单的例子来更好地理解它。
示例 - 1
陈述 -
所有工程师都是傻瓜。所有傻瓜都是医生。所有医生都是穷人。
结论 -
I. 一些穷人是傻瓜。
II. 一些穷人是工程师。
选项 -
A - 只有 I 有效
B - 只有 II 有效
C - 两个陈述都有效
D - 两个陈述均无效
答案 - 选项 C
解释 -
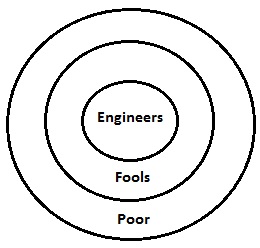
给定陈述的韦恩图如上所示。它以图解的方式将所有陈述集中在一个地方。现在,如果我们逐一讨论结论,一切都会变得清晰。
这里傻瓜是穷人的子集。因此,很明显一些穷人将是傻瓜。因此,结论 I 有效。同样,结论 II 有效,因为工程师也是穷人的子集。因此,两个陈述都有效。
示例 - 2
陈述 -
一些键盘是鼠标。一些鼠标是收音机。
结论 -
I. 一些键盘是收音机。
II. 一些收音机是键盘
III. 所有收音机都是鼠标。
IV. 所有鼠标都是键盘。
选项 -
A - 只有结论 I 有效
B - 只有结论 II 有效
C - I 或 II 有效
D - 没有结论有效
E - I 和 II 均有效
答案 - 选项 D
解释 - 由于两个陈述都是特定的,因此没有明确的结论有效。
示例 - 3
陈述 -
所有学生都是清醒的。所有学生都是淘气的。
结论 -
I. 所有淘气的要么是清醒的,要么反之亦然。
II. 一些清醒的人是淘气的。
III. 通常淘气的人是清醒的。
IV. 犯罪和内疚是相伴而生的。
选项 -
A - 只有结论 I 有效
B - 只有结论 II 有效
C - I 或 II 有效
D - I 或 II 均无效
E - I 和 II 均有效
答案 - 选项 B
解释 - 由于中间项“学生”在陈述中被分配了两次,因此结论不能太宽泛。因此,有效的是“一些清醒的人是淘气的”。因此,II 成立。
