推理 - 正方体和长方体
如今,几乎每场竞争性考试都会出现一些基于“正方体和长方体”的问题。这些问题在各种竞争性考试中非常常见。
下面描述的方法既简单又优雅。它们应该非常容易理解,并且只要稍微练习一下,你就能掌握它们。正方体是一个三维立体,具有 6 个面、12 条边和 8 个角。正方体的所有边都相等,所有面都是正方形。即一个具有 6 个面的立体图形;每个面都是正方形,称为正方体。如果六个面都是长方形,则称为长方体。长方体也称为直角平行六面体。
关于正方体和长方体的问题可能属于以下类型。
类型 I
给出完整正方体的几个视图,你必须找到正方体的哪个部分正好位于特定部分的下方。
类型 II
给出展开的正方体,你必须预测它在折叠成正方体后会是什么样子。
类型 III
一个正方体可能没有或在其某些面上用相同颜色或不同颜色涂漆,然后将其切割成一定数量的相同小块。然后问题形式为:“有多少个小正方体有 2 个面涂漆?”“有多少个小正方体只有一个面涂漆?”等等。
考试中出现两种类型的题目。首先,给你一个完整正方体的几个视图,你必须说明正方体的哪个部分正好位于特定部分的下方。在另一种类型中,给你一个展开的正方体,你必须预测它在折叠成正方体后会是什么样子。
例如 -
正方体的几个面如下所示 -

哪个数字与 2 相对?
A - 1
B - 6
C - 5
D - 4
基本方法如下 -
类型 I
基本规则:相对面不能在一起;
每当我们看到一个正方体,只有三个面可见时,我们永远无法看到两个相对面在一起。有了所有这些规则,我们就可以轻松解决上面讨论的问题类型。在上述问题中,我们需要找到特定面的相对面,我们可以排除那些在任何视图中与 X 同时出现的那些面。因此,我们可以排除所有其他选择,剩下的就是我们的答案。
此时,你应该再次通读上一段,并确保你理解了这个概念。之后,你应该尝试解决上述示例,看看是否能应用上面讨论的概念。但是,如果你发现自己没有完全理解这个概念,也没关系。继续阅读本节内容。一旦你完成本节内容,事情就会变得清晰起来。牢记上述基本规则,你可以解决上述类型的问题。
对于这个问题,规则本身就足够了。之后,你可以通过三个次要规则更快地解决它。
上述示例的解决方案 -
在给定的示例中,我们需要找到与 2 相对的面。现在在第一个图形中,2 与 1 和 3 一起出现。这意味着 1 和 3 都不能与 2 相对。这意味着与 1 相对可以是 4 或 5 或 6。类似地,与 3 相对可以是 4 或 5 或 6。现在,看看第二个图形。在这里,3 和 1 与 5 同时出现。这意味着 5 既不是与 3 相对也不是与 1 相对。所以,这意味着 4 或 6 与 1 相对,另一个与 3 相对,所以 5 必须与 2 相对。因此 5 是正确答案。
一些更快的规则
现在你必须已经理解了解决此类问题的基本技巧。技巧是,你应该排除那些不可能的选择。为此,你可以借助基本规则,该规则指出,如果两个面彼此相对,则它们不可能在一个正方体的视图中同时出现。然而,在当今时间宝贵的竞争中,仅仅依靠概念是不够的。你必须能够快速解决问题。有一些次要规则可以用来解决问题。
规则 I - 我们称那个需要找到其相对面的图形为 X。假设在正方体的任何一个视图中,X 与 Y 和 Z 一起出现。连同第三个图形(例如 A),则 X 将与 A 相对。
例如,你需要找到与 2 相对的面。(这是我们的 X)。现在,2 在一个图形中与 1 和 3 一起出现。(Y 和 Z)。此外,1 和 3 在另一个图形中一起出现,与 5 一起出现。(即 A)。因此,2 必须与 5 相对。
规则 II - 我们需要找到‘X’的相对面。假设在正方体的任何一个视图中,X 与 Y 和 Z 一起出现。现在,假设 Y 和 Z 在任何其他视图中都不一起出现,但它们在两个或多个不同的视图中分别出现。那么,Y 和 Z 分别出现的两个或多个不同视图之间的公共图形将是与 X 相对的图形。
规则 III - 我们称需要找到其相对面的图形为 X。现在,假设 X 出现在两个视图中,并且在这两个视图中,可以看到四个不同的图形与 X 一起出现。那么,在这两个视图中没有与 X 一起出现的唯一图形必须与 X 相对。
总结 - 你必须牢记基本规则,然后应用三个次要规则来快速回答。整个方法可以通过以下图表进行总结。
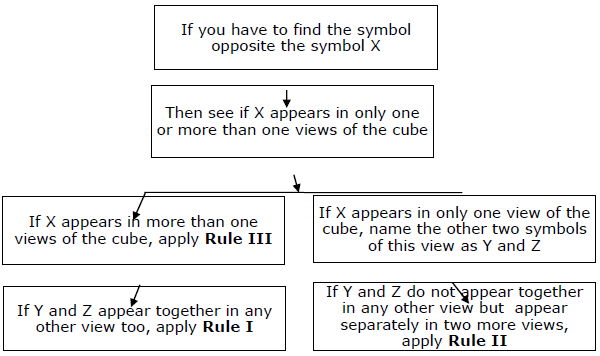
类型 II
在这种类型中,我们使用基本规则。此规则帮助我们排除那些在单个视图中显示相对面的组合。因此,如果我们知道如何通过查看“展开的正方体”来确定哪些面彼此相对,它将导致排除一个选择。为此,有一个非常简单的规则,通过该规则,你只需查看展开的正方体,就可以通过查看它来判断哪些面彼此相对。
规则如下;
第三个相对规则 -
当你想找出某个面的相对面(例如 X)时,在图 I、II、III 中;给出一个展开的正方体。我们需要找到当正方体闭合时哪些面彼此相对。
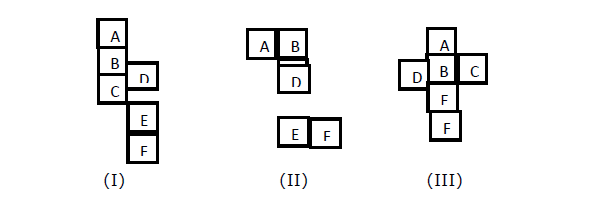
解释 -
在图 (I) 中,A 的第三个图形是 C。所以 A 与 C 相对。所以,D 和 F 将彼此相对。B 和 E 将彼此相对。
在图 (II) 中,B 是 D 的第三个图形,所以 B 将与 D 相对。类似地,C 将与 E 相对,A 将与 F 相对。
在图 (III) 中,A 与 E 相对,B 与 F 相对。因此,C 与 D 相对。
解决问题的步骤
我们现在可以解决此类型的题目。我们知道如何通过查看展开的正方体来找到相对面。我们也知道,在正方体的任何视图中,相对面都不能在一起。因此,结合这两个规则,我们可以轻松解决问题。
总结
至此,关于如何解决类型 II 问题的讨论就完成了。你必须使用“第三个相对规则”来确定哪些面彼此相对。下图将提供有关此方法的完整信息。
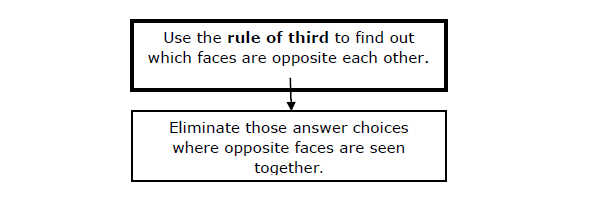
类型 III
正方体的计数(当涂漆的实心正方体被切割时);
在上一节中,我们讨论了查找正方体相对面的问题。还有另一种与正方体相关的问题,其中一个较大的正方体在其不同侧面涂有不同的颜色,被分成几个较小的正方体,你必须找到只有一个侧面涂漆或两个侧面涂漆的正方体的数量。
此问题的格式 -
示例 -
一个正方体的侧面涂有三种颜色:绿色、蓝色和红色,每种颜色都涂在正方体的相对面上。现在,将正方体分成 64 个大小相等的小正方体。根据这些信息,回答以下问题 -
1. 有多少个小正方体有两个面涂漆,其余面未涂漆?
A - 18
B - 20
C - 22
D - 24
2. 有多少个小正方体只有一个面涂漆(仅为绿色或蓝色)?
A - 4
B - 24
C - 16
D - 12
3. 有多少个小正方体没有侧面涂漆?
A - 0
B - 8
C - 12
D - 64
