数字信号处理 - 基本连续时间信号

---

---

为了测试系统，通常使用标准或基本信号。这些信号是许多复杂信号的基本组成部分。因此，它们在信号和系统研究中扮演着非常重要的角色。

单位冲激信号或狄拉克函数

满足条件$\delta(t) = \lim_{\epsilon \to 0} x(t)$的信号称为单位冲激信号。该信号在t=0时趋于无穷大，在t≠0时趋于零，其曲线下的面积始终等于1。除了t=0点外，狄拉克函数在其他任何地方的幅度都为零。

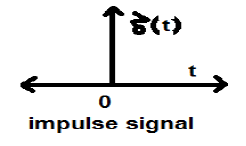
单位冲激信号的特性

• δ(t)是偶函数。
• δ(t)是非能量非功率(NENP)信号。
• 单位冲激信号的面积可以写成：
$$A = \int_{-\infty}^{\infty} \delta (t)dt = \int_{-\infty}^{\infty} \lim_{\epsilon \to 0} x(t) dt = \lim_{\epsilon \to 0} \int_{-\infty}^{\infty} x(t)dt = 1$$
• 信号的权重或强度可以写成：
$$y(t) = A\delta (t)$$
• 加权冲激信号的面积可以写成：
$$y (t) = \int_{-\infty}^{\infty} y (t)dt = \int_{-\infty}^{\infty} A\delta (t) = A[\int_{-\infty}^{\infty} \delta (t)dt ] = A$$

单位阶跃信号

满足以下两个条件的信号：

• $U(t) = 1(当\quad t \geq 0)$且
• $U(t) = 0 (当\quad t < 0)$

称为单位阶跃信号。

它具有在t=0处显示不连续性的特性。在不连续点，信号值由信号值平均值给出。该信号是在不连续点之前和之后取的（根据吉布斯现象）。

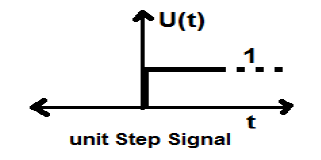
如果我们将一个阶跃信号添加到另一个经过时间缩放的阶跃信号，则结果将为1.它是一种功率型信号，功率值为0.5。均方根(RMS)值为0.707，平均值也为0.5。

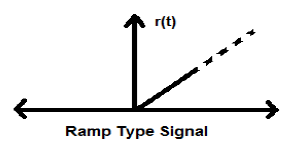
斜坡信号

阶跃信号的积分产生斜坡信号。它用r(t)表示。斜坡信号也满足条件$r(t) = \int_{-\infty}^{t} U(t)dt = tU(t)$。它是非能量非功率(NENP)型信号。

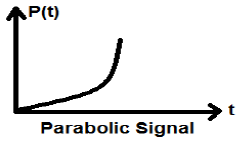
抛物线信号

斜坡信号的积分导致抛物线信号。它用p(t)表示。抛物线信号也满足条件$p(t) = \int_{-\infty}^{t} r(t)dt = (t^{2}/2)U(t)$。它是非能量非功率(NENP)型信号。

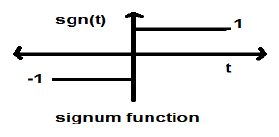
符号函数

此函数表示为

$$sgn(t) = \begin{cases}1 & 当\quad t >0\\-1 & 当\quad t<0\end{cases}$$

它是一种功率型信号。其功率值和均方根(RMS)值均为1。符号函数的平均值为零。

Sinc函数

它也是正弦函数，写成：

$$SinC(t) = \frac{Sin\Pi t}{\Pi t} = Sa(\Pi t)$$

Sinc函数的特性

• 它是一种能量型信号。

• $Sinc(0) = \lim_{t \to 0}\frac{\sin \Pi t}{\Pi t} = 1$

• $Sinc(\infty) = \lim_{t \to \infty}\frac{\sin \Pi \infty}{\Pi \infty} = 0$（sinπ∞的范围在-1到+1之间，但任何数除以无穷大都等于零）

• 如果$ \sin c(t) = 0 => \sin \Pi t = 0$

  $\Rightarrow \Pi t = n\Pi$

  $\Rightarrow t = n (n \neq 0)$

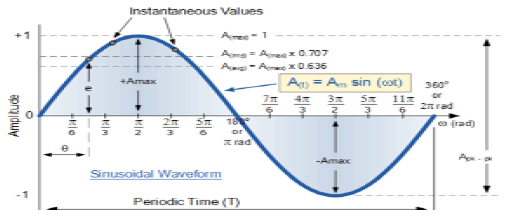
正弦信号

连续性质的信号称为连续信号。正弦信号的一般形式为

$$x(t) = A\sin (\omega t + \phi )$$

这里，

A = 信号的幅度

ω = 信号的角频率（以弧度为单位测量）

φ = 信号的相位角（以弧度为单位测量）

该信号倾向于在一定时间段后重复自身，因此称为周期信号。信号的周期为：

$$T = \frac{2\pi }{\omega }$$

正弦信号的示意图如下所示。

矩形函数

如果信号满足以下条件，则称为矩形函数类型：

$$\pi(\frac{t}{\tau}) = \begin{cases}1, & 当\quad |t|\leq \frac{\tau}{2}\\0, & 其他情况\end{cases}$$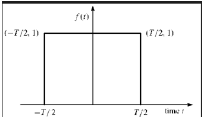

由于关于Y轴对称，因此该信号称为偶函数。

三角脉冲信号

任何满足以下条件的信号都称为三角信号。

$$\Delta(\frac{t}{\tau}) = \begin{cases}1-(\frac{2|t|}{\tau}) & 当|t|<\frac{\tau}{2}\\0 & 当|t|>\frac{\tau}{2}\end{cases}$$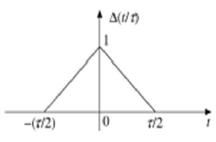

该信号关于Y轴对称。因此，它也称为偶函数。