数字信号处理 - 其他信号

---

---

还有一些其他信号，它们是通过对信号进行运算得到的。下面讨论一些常见的信号类型。

共轭信号

满足条件$x(t) = x*(-t)$的信号称为共轭信号。

设 $x(t) = a(t)+jb(t)$...式1

则，$x(-t) = a(-t)+jb(-t)$

以及 $x*(-t) = a(-t)-jb(-t)$...式2

根据条件，$x(t) = x*(-t)$

比较式1和式2，我们可以看到实部是偶函数，虚部是奇函数。这是信号为共轭类型的条件。

共轭反对称信号

满足条件$x(t) = -x*(-t)$的信号称为共轭反对称信号。

设 $x(t) = a(t)+jb(t)$...式1

则 $x(-t) = a(-t)+jb(-t)$

以及 $x*(-t) = a(-t)-jb(-t)$

$-x*(-t) = -a(-t)+jb(-t)$...式2

根据条件 $x(t) = -x*(-t)$

现在，再次比较这两个方程，就像我们对共轭信号所做的那样。在这里，我们将发现实部是奇函数，虚部是偶函数。这是信号成为共轭反对称类型的条件。

示例

设给定信号为$x(t) = \sin t+jt^{2}$。

这里，实部$\sin t$是奇函数，虚部$t^2$是偶函数。因此，此信号可以分类为共轭反对称信号。

任何函数都可以分成两部分。一部分是共轭对称，另一部分是共轭反对称。因此，任何信号x(t)都可以写成

$$x(t) = xcs(t)+xcas(t)$$

其中$xcs(t)$是共轭对称信号，$xcas(t)$是共轭反对称信号

$$xcs(t) = \frac{[x(t)+x*(-t)]}{2}$$

以及

$$xcas(t) = \frac{[x(t)-x*(-t)]}{2}$$

半波对称信号

当信号满足条件$cx(t) = -x(t\pm (\frac{T_{0}}{2}))$时，称为半波对称信号。这里，信号发生幅度反转和时间位移，位移量为半个周期。对于半波对称信号，平均值为零，但反过来则不然。

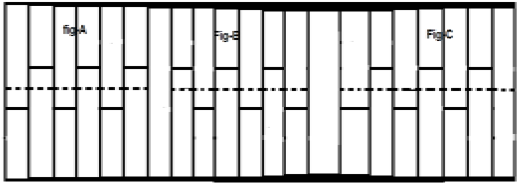
考虑上图A所示的信号x(t)。第一步是对信号进行时间位移，使其变为$x[t-(\frac{T}{2})]$。因此，新的信号如B图所示。接下来，我们反转信号的幅度，即使其变为$-x[t-(\frac{T}{2})]$，如C图所示。由于此信号在半个周期位移和幅度反转后重复自身，因此它是一个半波对称信号。

正交信号

如果两个信号x(t)和y(t)满足以下两个条件，则称它们为正交信号。

条件1 − $\int_{-\infty}^{\infty}x(t)y(t) = 0$ [对于非周期信号]

条件2 − $\int x(t)y(t) = 0$ [对于周期信号]

包含奇次谐波（3次、5次、7次……等）且具有不同频率的信号彼此互为正交。

在三角函数类型的信号中，正弦函数和余弦函数也彼此正交；前提是它们具有相同的频率和相位。同样，直流（直流信号）和正弦信号也彼此正交。如果x(t)和y(t)是两个正交信号，且$z(t) = x(t)+y(t)$，则z(t)的功率和能量可以写成：

$$P(z) = p(x)+p(y)$$ $$E(z) = E(x)+E(y)$$

示例

分析信号：$z(t) = 3+4\sin(2\pi t+30^0)$

这里，信号包含一个直流信号(3)和一个正弦函数。因此，根据此性质，该信号是正交信号，其中的两个子信号彼此互为正交。