
- 数字信号处理教程
- 数字信号处理 - 首页
- 数字信号处理 - 信号定义
- 数字信号处理 - 基本连续时间信号
- 数字信号处理 - 基本离散时间信号
- 数字信号处理 - 连续时间信号分类
- 数字信号处理 - 离散时间信号分类
- 数字信号处理 - 其他信号
- 基本系统特性
- 数字信号处理 - 静态系统
- 数字信号处理 - 动态系统
- 数字信号处理 - 因果系统
- 数字信号处理 - 非因果系统
- 数字信号处理 - 反因果系统
- 数字信号处理 - 线性系统
- 数字信号处理 - 非线性系统
- 数字信号处理 - 时不变系统
- 数字信号处理 - 时变系统
- 数字信号处理 - 稳定系统
- 数字信号处理 - 不稳定系统
- 数字信号处理 - 例题解析
- 数字信号处理资源
- 数字信号处理 - 快速指南
- 数字信号处理 - 有用资源
- 数字信号处理 - 讨论
数字信号处理 - DFT分段卷积
假设,需要使用具有有限持续时间冲激响应的系统来处理长时间输入序列x(n),方法是将两个序列进行卷积。由于通过DFT执行的线性滤波涉及对固定大小的数据块进行运算,因此在处理之前,将输入序列划分为不同的固定大小的数据块。
然后一次处理连续的块,并将结果组合以产生净结果。
由于卷积是通过将长的输入序列划分为不同的固定大小的部分来执行的,因此它被称为分段卷积。在进行FIR滤波器处理之前,将长的输入序列分割成固定大小的块。
有两种方法可以评估离散卷积:
重叠保存法
重叠相加法
重叠保存法
重叠保存是一种评估非常长的信号x(n)和有限脉冲响应(FIR)滤波器h(n)之间的离散卷积的有效方法的传统名称。以下是重叠保存法的步骤:
设输入数据块长度 = N = L+M-1。因此,DFT和IDFT长度 = N。每个数据块包含前一个块的M-1个数据点,然后是L个新的数据点,形成长度为N = L+M-1的数据序列。
首先,计算每个数据块的N点DFT。
通过附加(L-1)个零,FIR滤波器的冲激响应长度增加,并计算和存储N点DFT。
两个N点DFT H(k)和Xm(k)的乘法:Y′m(k) = H(k).Xm(k),其中K=0,1,2,…N-1
然后,IDFT[Y′m((k)] = y′((n) = [y′m(0), y′m(1), y′m(2),.......y′m(M-1), y′m(M),.......y′m(N-1)]
(此处,N-1 = L+M-2)
由于混叠,前M-1个点被破坏,因此由于数据记录的长度为N,因此将其丢弃。
最后L个点与卷积的结果完全相同,因此
y′m (n) = ym(n) 其中 n = M, M+1,….N-1
为了避免混叠,保存每个数据记录的最后M-1个元素,这些点将传递到后续记录并成为前M-1个元素。
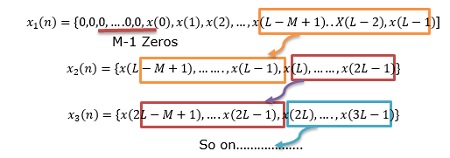
IDFT的结果,其中避免了前M-1个点以消除混叠,其余L个点构成了与线性卷积相同的期望结果。
重叠相加法
以下是使用重叠相加法求解离散卷积的步骤:
设输入数据块大小为L。因此,DFT和IDFT的大小:N = L+M-1
每个数据块在最后附加M-1个零。
计算N点DFT。

两个N点DFT相乘:Ym(k) = H(k).Xm(k),其中k = 0,,1,2,….,N-1
IDFT [Ym(k)]产生长度为N的块,这些块不受混叠的影响,因为DFT的大小为N = L+M-1,并且通过向每个块附加M-1个零来将序列的长度增加到N点。
每个块的最后M-1个点必须与后续块的前M-1个点重叠并相加。
(原因:每个数据块以M-1个零结尾)
因此,这种方法被称为重叠相加法。因此,我们得到:
y(n) = {y1(0), y1(1), y1(2), ... .., y1(L-1), y1(L)+y2(0), y1(L+1)+y2(1), ... ... .., y1(N-1)+y2(M-1),y2(M), ... ... ... ... ... }