数字信号处理 - 基本离散时间信号

---

---

我们已经了解了如何在连续时间域表示基本信号。让我们看看如何在离散时间域表示基本信号。

单位脉冲序列

在离散时间域中表示为 δ(n)，其定义如下：

$$\delta(n)=\begin{cases}1, & for \quad n=0\\0, & Otherwise\end{cases}$$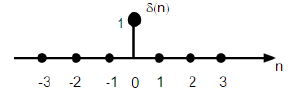

单位阶跃信号

离散时间单位阶跃信号定义如下：

$$U(n)=\begin{cases}1, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$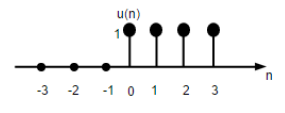

上图显示了离散阶跃函数的图形表示。

单位斜坡函数

离散单位斜坡函数可以定义为：

$$r(n)=\begin{cases}n, & for \quad n\geq0\\0, & for \quad n<0\end{cases}$$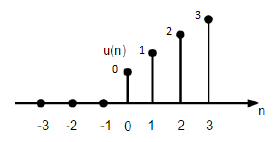

上图显示了离散斜坡信号的图形表示。

抛物线函数

离散单位抛物线函数表示为 p(n)，其定义如下：

$$p(n) = \begin{cases}\frac{n^{2}}{2} ,& for \quad n\geq0\\0, & for \quad n<0\end{cases}$$

用单位阶跃函数表示为：

$$P(n) = \frac{n^{2}}{2}U(n)$$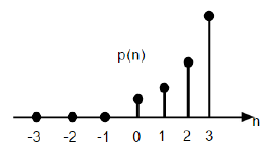

上图显示了抛物线序列的图形表示。

正弦信号

所有连续时间信号都是周期性的。离散时间正弦序列可能是周期性的，也可能不是周期性的。这取决于 ω 的值。对于离散时间信号要成为周期性的，角频率 ω 必须是 2π 的有理数倍。

上图显示了一个离散正弦信号。

离散正弦信号可以表示为以下格式：

$$x(n) = A\sin(\omega n + \phi)$$

这里 A、ω 和 φ 具有其通常的含义，n 是整数。离散正弦信号的周期由下式给出：

$$N =\frac{2\pi m}{\omega}$$

其中，N 和 m 是整数。