
- 数字信号处理教程
- 数字信号处理 - 首页
- 数字信号处理 - 信号定义
- 数字信号处理 - 基本 CT 信号
- 数字信号处理 - 基本 DT 信号
- 数字信号处理 - CT 信号分类
- 数字信号处理 - DT 信号分类
- 数字信号处理 - 其他信号
- 基本系统特性
- 数字信号处理 - 静态系统
- 数字信号处理 - 动态系统
- 数字信号处理 - 因果系统
- 数字信号处理 - 非因果系统
- 数字信号处理 - 反因果系统
- 数字信号处理 - 线性系统
- 数字信号处理 - 非线性系统
- 数字信号处理 - 时不变系统
- 数字信号处理 - 时变系统
- 数字信号处理 - 稳定系统
- 数字信号处理 - 不稳定系统
- 数字信号处理 - 例题解析
- 数字信号处理资源
- 数字信号处理 - 快速指南
- 数字信号处理 - 有用资源
- 数字信号处理 - 讨论
数字信号处理 - CT 信号分类
连续时间信号可以根据不同的条件或对信号执行的操作进行分类。
偶信号和奇信号
偶信号
如果信号满足以下条件,则称其为偶信号:
x(−t)=x(t)这里,信号的时间反转不会导致幅度发生任何变化。例如,考虑下面所示的三角波。
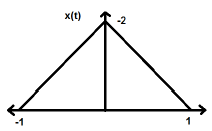
三角信号是偶信号,因为它关于 Y 轴对称。我们可以说它是关于 Y 轴的镜像。
考虑下图所示的另一个信号。
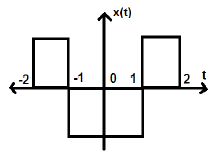
我们可以看到,上述信号是偶信号,因为它关于 Y 轴对称。
奇信号
如果信号满足以下条件,则称其为奇信号:
x(−t)=−x(t)这里,时间反转和幅度变化同时发生。
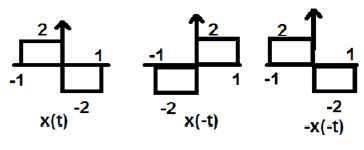
在上图中,我们可以看到一个阶跃信号 x(t)。为了测试它是否是奇信号,我们首先进行时间反转,即 x(-t),结果如上图所示。然后我们反转所得信号的幅度,即 –x(-t),结果如上图所示。
如果我们比较第一个和第三个波形,我们可以看到它们是相同的,即 x(t)= -x(-t),这满足我们的条件。因此,上述信号是奇信号。
一些与偶信号和奇信号相关的重要的结果如下所示。
- 偶 × 偶 = 偶
- 奇 × 奇 = 偶
- 偶 × 奇 = 奇
- 偶 ± 偶 = 偶
- 奇 ± 奇 = 奇
- 偶 ± 奇 = 既非偶也非奇
将任何信号表示为偶数或奇数形式
有些信号不能直接分类为偶数或奇数类型。它们表示为偶数和奇数信号的组合。
x(t)→xe(t)+x0(t)其中 xe(t) 表示偶信号,xo(t) 表示奇信号
xe(t)=[x(t)+x(−t)]2和
x0(t)=[x(t)−x(−t)]2示例
求信号 x(n)=t+t2+t3 的偶数和奇数部分
解 − 反转 x(n),我们得到
x(−n)=−t+t2−t3
现在,根据公式,偶数部分
xe(t)=x(t)+x(−t)2
=[(t+t2+t3)+(−t+t2−t3)]2
=t2
类似地,根据公式,奇数部分是
x0(t)=[x(t)−x(−t)]2
=[(t+t2+t3)−(−t+t2−t3)]2
=t+t3
周期信号和非周期信号
周期信号
周期信号在一定时间间隔后重复自身。我们可以用等式形式表示为:
x(t)=x(t)±nT其中,n = 整数 (1,2,3……)
T = 基波周期 (FTP) ≠ 0 且 ≠∞
基波周期 (FTP) 是信号具有周期性的最小正定值。
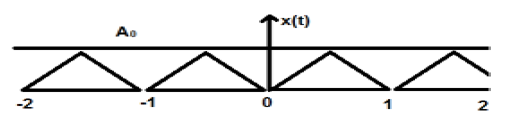
上图显示了一个幅度为 A 的三角信号。这里,信号每 1 秒重复一次。因此,我们可以说该信号是周期性的,其 FTP 为 1 秒。
非周期信号
简单地说,我们可以说,不是周期性的信号本质上是非周期性的。显然,这些信号不会在任何时间间隔后重复自身。
非周期信号不遵循一定的格式;因此,没有特定的数学方程可以描述它们。
Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.
能量信号和功率信号
当且仅当包含的总能量有限且非零 (0<E<∞) 时,信号被称为能量信号。因此,对于任何能量型信号,总归一化信号都是有限且非零的。
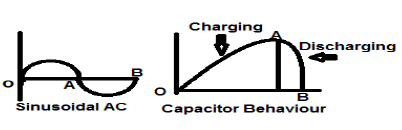
正弦交流电流信号是能量型信号的完美示例,因为它在一种情况下处于正半周期,而在下一半周期则为负。因此,其平均功率变为零。
无损电容器也是能量型信号的完美示例,因为它在连接到电源时会充电到最佳水平,并且当电源移除时,它会通过负载耗散等量的能量,使其平均功率为零。
对于任何有限信号 x(t),能量可以表示为 E,并写成:
E=∫+∞−∞x2(t)dt能量型信号的频谱密度给出了分布在各个频率水平上的能量量。
功率型信号
当且仅当归一化平均功率有限且非零,即 (0<p<∞) 时,信号被称为功率型信号。对于功率型信号,归一化平均功率是有限且非零的。几乎所有周期信号都是功率信号,它们的平均功率是有限且非零的。
用数学形式表示,信号 x(t) 的功率可以写成:
P=limT→∞1/T∫+T/2−T/2x2(t)dt能量信号和功率信号的区别
下表总结了能量信号和功率信号的区别。
| 功率信号 | 能量信号 |
|---|---|
| 实际的周期信号是功率信号。 | 非周期信号是能量信号。 |
| 这里,归一化平均功率有限且非零。 | 这里,总归一化能量有限且非零。 |
|
数学上, P=limT→∞1/T∫+T/2−T/2x2(t)dt |
数学上, E=∫+∞−∞x2(t)dt |
| 这些信号的存在时间是无限的。 | 这些信号存在于有限的时间段内。 |
| 功率信号的能量在无限时间内是无限的。 | 能量信号的功率在无限时间内为零。 |
例题解析
例 1 − 求信号 z(t)=2cos(3Πt+30o)+4sin(3Π+30o) 的功率
解 − 上述两个信号彼此正交,因为它们的频率项彼此相同,并且它们具有相同的相位差。因此,总功率将是各个功率的总和。
设 z(t)=x(t)+y(t)
其中 x(t)=2cos(3Πt+30o) 和 y(t)=4sin(3Π+30o)
x(t) 的功率 = 222=2
y(t) 的功率 = 422=8
因此,P(z)=p(x)+p(y)=2+8=10…答案。
例 2 − 测试给定信号 x(t)=t2+jsint 是否为共轭信号?
解 − 这里,实部 t2 为偶数,虚部 (虚部) sint 为奇数。所以上述信号是共轭信号。
例 3 − 验证 X(t)=sinωt 是否为奇信号或偶信号。
解 − 给定 X(t)=sinωt
通过时间反转,我们将得到 sin(−ωt)
但我们知道 sin(−ϕ)=−sinϕ。
因此,
sin(−ωt)=−sinωt这满足信号为奇信号的条件。因此,sinωt 是奇信号。