数字信号处理 - 线性系统

线性系统遵循叠加原理。该定律是证明系统线性的充分必要条件。除此之外，该系统是两种定律的组合：

• 可加性定律
• 齐次性定律

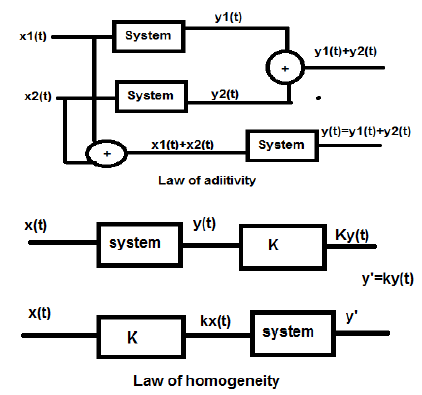
上述图形显示了齐次性定律和可加性定律。但是，还有一些其他条件可以用来检查系统是否线性。

条件如下：

• 零输入时输出应为零。
• 系统中不应存在任何非线性算子。

非线性算子的例子：

(a) 三角函数算子 - 正弦、余弦、正切、余切、正割、余割等。

(b) 指数、对数、模、平方、立方等。

(c) sa(输入), sinc(输入), sqn(输入) 等。

输入 x 或输出 y 不应包含这些非线性算子。

示例

让我们找出以下系统是否是线性的。

a) $y(t) = x(t)+3$

该系统不是线性系统，因为它违反了第一个条件。如果我们将输入设为零，即 x(t) = 0，则输出不为零。

b) $y(t) = \sin tx(t)$

在这个系统中，如果我们输入为零，输出将变为零。因此，第一个条件显然满足。同样，没有对 x(t) 应用任何非线性算子。因此，第二个条件也满足。因此，该系统是线性系统。

c) $y(t) = \sin (x(t))$

在上述系统中，第一个条件满足，因为如果我们设 x(t) = 0，输出也将为 sin(0) = 0。但是，第二个条件不满足，因为存在对 x(t) 进行运算的非线性算子。因此，该系统不是线性的。