DSP - 离散时间信号的分类

---

---

就像连续时间信号一样，离散时间信号可以根据信号的条件或运算进行分类。

偶信号和奇信号

偶信号

如果信号满足以下条件，则称该信号为偶信号或对称信号：

$$x(-n) = x(n)$$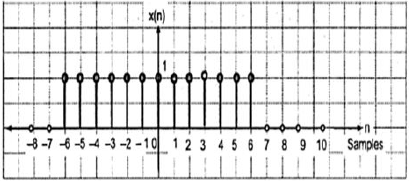

这里，我们可以看到 x(-1) = x(1)，x(-2) = x(2) 以及 x(-n) = x(n)。因此，这是一个偶信号。

奇信号

如果信号满足以下条件，则称该信号为奇信号：

$$x(-n) = -x(n)$$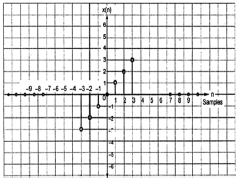

从图中我们可以看到 x(1) = -x(-1)，x(2) = -x(2) 以及 x(n) = -x(-n)。因此，它是一个奇信号，也是一个反对称信号。

周期信号和非周期信号

离散时间信号是周期性的，当且仅当它满足以下条件：

$$x(n+N) = x(n)$$

这里，x(n) 信号在 N 周期后重复自身。这可以通过考虑余弦信号来最好地理解：

$$x(n) = A \cos(2\pi f_{0}n+\theta)$$ $$x(n+N) = A\cos(2\pi f_{0}(n+N)+\theta) = A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$ $$= A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta)$$

为了使信号成为周期性的，应满足以下条件：

$$x(n+N) = x(n)$$ $$\Rightarrow A\cos(2\pi f_{0}n+2\pi f_{0}N+\theta) = A \cos(2\pi f_{0}n+\theta)$$

即 $2\pi f_{0}N$ 是 $2\pi$ 的整数倍

$$2\pi f_{0}N = 2\pi K$$ $$\Rightarrow N = \frac{K}{f_{0}}$$

离散正弦信号的频率间隔为 $2\pi$ 的整数倍。

能量信号和功率信号

能量信号

离散时间信号的能量表示为 E。在数学上，它可以写成：

$$E = \displaystyle \sum\limits_{n=-\infty}^{+\infty}|x(n)|^2$$

如果对 $x(n)$ 的每个单独值进行平方并相加，我们得到能量信号。这里 $x(n)$ 是能量信号，其能量在时间上是有限的，即 $0< E< \infty$

功率信号

离散信号的平均功率表示为 P。在数学上，这可以写成：

$$P = \lim_{N \to \infty} \frac{1}{2N+1}\displaystyle\sum\limits_{n=-N}^{+N} |x(n)|^2$$

这里，功率是有限的，即 0<P<∞。但是，也有一些信号既不属于能量信号也不属于功率信号。