数字信号处理 - 信号运算 卷积

---

---

两个信号在时域的卷积等效于它们在频域表示的乘积。数学上，我们可以将两个信号的卷积写成

$$y(t) = x_{1}(t)*x_{2}(t)$$ $$= \int_{-\infty}^{\infty}x_{1}(p).x_{2}(t-p)dp$$

卷积步骤

• 取信号x₁(t)并将t=p代入，使其变为x₁(p)。
• 取信号x₂(t)，执行步骤1，使其变为x₂(p)。
• 对信号进行折叠，即x₂(-p)。
• 对上述信号进行时间平移x₂[-(p-t)]
• 然后将两个信号相乘，即$x_{1}(p).x_{2}[−(p−t)]$

示例

让我们计算一个阶跃信号u(t)与其自身的卷积。

$y(t) = u(t)*u(t)$

$= \int_{-\infty}^{\infty}[u(p).u[-(p-t)]dp$

现在这个t可以大于或小于零，如下面的图形所示

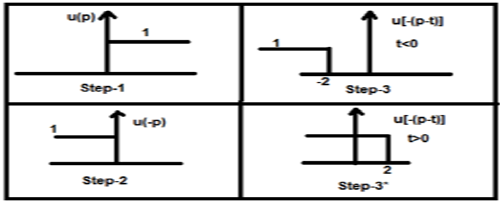
因此，根据上述情况，结果出现以下可能性

$y(t) = \begin{cases}0, & if\quad t<0\\\int_{0}^{t}1dt, & for\quad t>0\end{cases}$

$= \begin{cases}0, & if\quad t<0\\t, & t>0\end{cases} = r(t)$

卷积的性质

交换律

它指出卷积的顺序无关紧要，这可以用数学方式表示为

$$x_{1}(t)*x_{2}(t) = x_{2}(t)*x_{1}(t)$$

结合律

它指出涉及三个信号的卷积顺序可以是任意的。数学上，可以表示为：

$$x_{1}(t)*[x_{2}(t)*x_{3}(t)] = [x_{1}(t)*x_{2}(t)]*x_{3}(t)$$

分配律

可以先将两个信号相加，然后将其卷积与第三个信号进行卷积。这等效于将两个信号分别与第三个信号进行卷积，然后最终相加。数学上，这可以写成：

$$x_{1}(t)*[x_{2}(t)+x_{3}(t)] = [x_{1}(t)*x_{2}(t)+x_{1}(t)*x_{3}(t)]$$

面积

如果一个信号是两个信号卷积的结果，则该信号的面积是这两个信号面积的乘积。数学上可以写成

如果 $y(t) = x_{1}*x_{2}(t)$

则， y(t)的面积 = x₁(t)的面积 × x₂(t)的面积

尺度变换

如果两个信号按某个未知常数“a”进行缩放，然后进行卷积，则结果信号也将按相同的常数“a”进行卷积，并将除以该数量，如下所示。

如果， $x_{1}(t)*x_{2}(t) = y(t)$

则， $x_{1}(at)*x_{2}(at) = \frac{y(at)}{a}, a \ne 0$

延迟

假设信号y(t)是两个信号x1(t)和x2(t)卷积的结果。如果这两个信号分别延迟t1和t2时间，则结果信号y(t)将延迟(t1+t2)。数学上，可以写成：

如果， $x_{1}(t)*x_{2}(t) = y(t)$

则， $x_{1}(t-t_{1})*x_{2}(t-t_{2}) = y[t-(t_{1}+t_{2})]$

例题解析

例1 - 求信号u(t-1)和u(t-2)的卷积。

解答 - 给定的信号是u(t-1)和u(t-2)。它们的卷积可以如下所示：

$y(t) = u(t-1)*u(t-2)$

$y(t) = \int_{-\infty}^{+\infty}[u(t-1).u(t-2)]dt$

$= r(t-1)+r(t-2)$

$= r(t-3)$

例2 - 求由下式给出的两个信号的卷积

$x_{1}(n) = \lbrace 3,-2, 2\rbrace $

$x_{2}(n) = \begin{cases}2, & 0\leq n\leq 4\\0, & x > elsewhere\end{cases}$

解答 -

x₂(n)可以解码为$x_{2}(n) = \lbrace 2,2,2,2,2\rbrace$ (起始点为0)

x₁(n)先前给出$= \lbrace 3,-2,3\rbrace = 3-2Z^{-1}+2Z^{-2}$

类似地， $x_{2}(z) = 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}$

结果信号为：

$X(Z) = X_{1}(Z)X_{2}(z)$

$= \lbrace 3-2Z^{-1}+2Z^{-2}\rbrace \times \lbrace 2+2Z^{-1}+2Z^{-2}+2Z^{-3}+2Z^{-4}\rbrace$

$= 6+2Z^{-1}+6Z^{-2}+6Z^{-3}+6Z^{-4}+6Z^{-5}$

对上述结果进行逆Z变换，我们将得到结果信号为

$x(n) = \lbrace 6,2,6,6,6,0,4\rbrace$ (起始点为0)

例3 - 确定以下两个信号的卷积：

$x(n) = \lbrace 2,1,0,1\rbrace$

$h(n) = \lbrace 1,2,3,1\rbrace$

解答 -

对信号进行Z变换，得到：

$x(z) = 2+Z^{-1}+Z^{-3}$

以及 $h(n) = 1+2Z^{-1}+3Z^{-2}+Z^{-3}$

现在，两个信号的卷积意味着它们的Z变换的乘积

也就是说 $Y(Z) = X(Z) \times h(Z)$

$= \lbrace 2+Z^{-1}+Z^{-3}\rbrace \times \lbrace 1+2Z^{-1}+3Z^{-2}+Z^{-3}\rbrace$

$= \lbrace 2+5Z^{-1}+8Z^{-2}+6Z^{-3}+3Z^{-4}+Z^{-5}\rbrace$ (修正了计算错误)

进行逆Z变换，结果信号可以写成：

$y(n) = \lbrace 2,5,8,6,3,1\rbrace$ (起始点为0) (修正了计算错误)