
- 数字信号处理教程
- 数字信号处理 - 首页
- 数字信号处理 - 信号定义
- 数字信号处理 - 基本连续时间信号
- 数字信号处理 - 基本离散时间信号
- 数字信号处理 - 连续时间信号分类
- 数字信号处理 - 离散时间信号分类
- 数字信号处理 - 其他信号
- 基本系统特性
- 数字信号处理 - 静态系统
- 数字信号处理 - 动态系统
- 数字信号处理 - 因果系统
- 数字信号处理 - 非因果系统
- 数字信号处理 - 反因果系统
- 数字信号处理 - 线性系统
- 数字信号处理 - 非线性系统
- 数字信号处理 - 时不变系统
- 数字信号处理 - 时变系统
- 数字信号处理 - 稳定系统
- 数字信号处理 - 不稳定系统
- 数字信号处理 - 例题解析
- 数字信号处理资源
- 数字信号处理 - 快速指南
- 数字信号处理 - 有用资源
- 数字信号处理 - 讨论
数字信号处理 - 信号微分运算
对信号进行的两个非常重要的运算分别是微分和积分。
微分
任何信号 x(t) 的微分表示该信号关于时间的斜率。数学上表示为:
$$x(t)\rightarrow \frac{dx(t)}{dt}$$在运放微分电路中,这种方法非常有用。我们可以很容易地通过图形方法对信号进行微分,而不是使用公式。然而,条件是信号必须是矩形或三角形类型的,这在大多数情况下都是如此。
| 原始信号 | 微分后的信号 |
|---|---|
| 斜坡信号 | 阶跃信号 |
| 阶跃信号 | 冲激信号 |
| 冲激信号 | 1 |
上表说明了信号微分后的情况。例如,斜坡信号微分后变成阶跃信号。类似地,单位阶跃信号变成冲激信号。
示例
假设给定的信号为 $x(t) = 4[r(t)-r(t-2)]$。绘制该信号时,它看起来像下面图形左侧所示的那样。现在,我们的目标是对给定的信号进行微分。
首先,我们将开始对给定的方程进行微分。我们知道斜坡信号微分后得到单位阶跃信号。
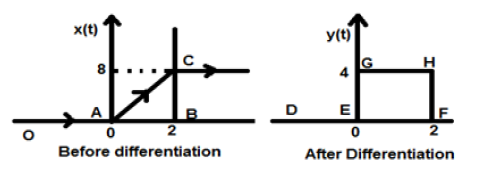
因此,我们的结果信号 y(t) 可以写成:
$y(t) = \frac{dx(t)}{dt}$
$= \frac{d4[r(t)-r(t-2)]}{dt}$
$= 4[u(t)-u(t-2)]$
现在,最终绘制了该信号,如上图右侧所示。
广告