数字信号处理 - 快速傅里叶变换

---

---

在之前的 DFT 方法中，我们看到计算部分过于冗长。我们需要减少它。这可以通过 FFT 或快速傅里叶变换来实现。所以，我们可以说 FFT 不过是离散傅里叶变换的算法化计算，其中计算量将会减少。

FFT 的主要优点在于，通过它我们可以设计 FIR 滤波器。从数学上讲，FFT 可以写成如下形式：

$$x[K] = \displaystyle\sum\limits_{n = 0}^{N-1}x[n]W_N^{nk}$$

让我们举个例子来更好地理解它。我们考虑了从 $x_0\quad 到\quad x_7$ 的八个点。我们将偶数项放在一组，奇数项放在另一组。上面提到的示意图如下所示：

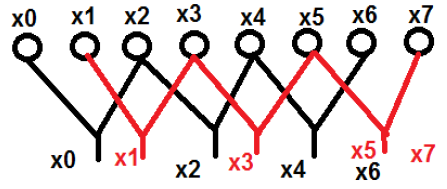
这里，点 x₀、x₂、x₄ 和 x₆ 被归为一类，类似地，点 x₁、x₃、x₅ 和 x₇ 被归为另一类。现在，我们可以进一步将它们分成两组，并继续进行计算。现在，让我们看看这些进一步分成两组是如何帮助计算的。

$x[k] = \displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r]W_N^{2rk}+\displaystyle\sum\limits_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_N^{(2r+1)k}$

$= \sum_{r = 0}^{\frac{N}{2}-1}x[2r]W_{N/2}^{rk}+\sum_{r = 0}^{\frac{N}{2}-1}x[2r+1]W_{N/2}^{rk}\times W_N^k$

$= G[k]+H[k]\times W_N^k$

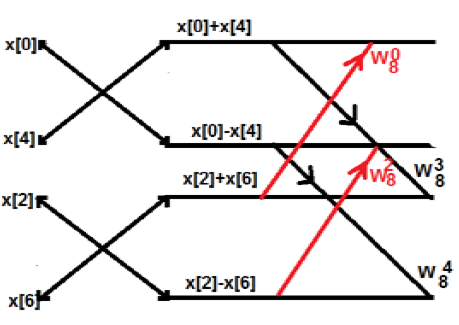
最初，我们取了一个八点序列，但后来我们将其分成两部分 G[k] 和 H[k]。G[k] 代表偶数部分，而 H[k] 代表奇数部分。如果我们想通过图表来实现它，那么它可以显示如下：

从上图可以看出

$W_8^4 = -1$

$W_8^5 = -W_8^1$

$W_8^6 = -W_8^2$

$W_8^7 = -W_8^3$

类似地，最终值可以写成如下形式：

$G[0]-H[0] = x[4]$

$G[1]-W_8^1H[1] = x[5]$

$G[2]-W_8^2H[2] = x[6]$

$G[1]-W_8^3H[3] = x[7]$

以上是一个周期性序列。该系统的缺点是 K 不能分解到 4 点以下。现在让我们将以上内容进一步分解。我们会得到类似这样的结构

示例

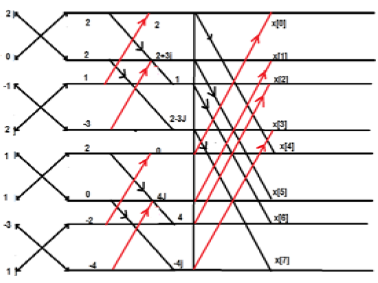
考虑序列 x[n]={ 2,1,-1,-3,0,1,2,1}。计算 FFT。

解答 - 给定的序列为 x[n]={ 2,1,-1,-3,0,1,2,1}

按如下所示排列项；