
- 数字信号处理教程
- 数字信号处理 - 首页
- 数字信号处理 - 信号定义
- 数字信号处理 - 基本连续时间信号
- 数字信号处理 - 基本离散时间信号
- 数字信号处理 - 连续时间信号分类
- 数字信号处理 - 离散时间信号分类
- 数字信号处理 - 其他信号
- 基本系统特性
- 数字信号处理 - 静态系统
- 数字信号处理 - 动态系统
- 数字信号处理 - 因果系统
- 数字信号处理 - 非因果系统
- 数字信号处理 - 反因果系统
- 数字信号处理 - 线性系统
- 数字信号处理 - 非线性系统
- 数字信号处理 - 时不变系统
- 数字信号处理 - 时变系统
- 数字信号处理 - 稳定系统
- 数字信号处理 - 不稳定系统
- 数字信号处理 - 例题解析
- 数字信号处理资源
- 数字信号处理 - 快速指南
- 数字信号处理 - 有用资源
- 数字信号处理 - 讨论
数字信号处理 - 信号缩放运算
信号缩放是指将一个常数乘以信号的时间或幅度。
时间缩放
如果将一个常数乘以时间轴,则称为时间缩放。这可以用数学方式表示为:
$x(t) \rightarrow y(t) = x(\alpha t)$ 或 $x(\frac{t}{\alpha})$; 其中 α ≠ 0
因此,y轴保持不变,x轴的幅度根据常数的符号(正或负)而减小或增大。因此,缩放也可以分为以下两类。
时间压缩
当alpha大于零时,信号的幅度被alpha除,而Y轴的值保持不变。这被称为时间压缩。
示例
让我们考虑一个信号x(t),如下图所示。让我们取alpha的值为2。所以,y(t)将是x(2t),如下图所示。
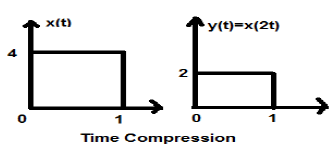
从上图可以清楚地看出,y轴的时间幅度保持不变,但x轴的幅度从4减小到2。因此,这是一个时间压缩的情况。
时间扩展
当时间除以常数alpha时,信号的Y轴幅度乘以alpha倍,而X轴幅度保持不变。因此,这称为时间扩展型信号。
示例
让我们考虑一个幅度为1的方波信号x(t)。当我们将其时间缩放一个常数3,使得$x(t) \rightarrow y(t) \rightarrow x(\frac{t}{3})$时,信号的幅度将乘以3倍,如下图所示。
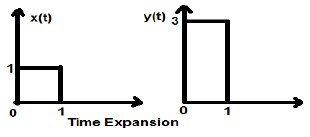
幅度缩放
将一个常数乘以信号的幅度会导致幅度缩放。根据常数的符号,它可以是幅度缩放或衰减。让我们考虑一个方波信号x(t) = Π(t/4)。
假设我们定义另一个函数y(t) = 2 Π(t/4)。在这种情况下,y轴的值将加倍,而时间轴的值保持不变。如下图所示。
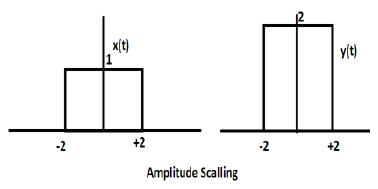
考虑另一个定义为z(t)的方波函数,其中z(t) = 0.5 Π(t/4)。这里,函数z(t)的幅度将是x(t)的一半,即时间轴保持不变,幅度轴将减半。如下图所示。
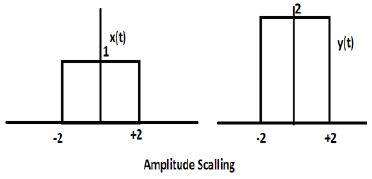
广告