
- 数字信号处理教程
- 数字信号处理 - 首页
- 数字信号处理 - 信号定义
- 数字信号处理 - 基本连续时间信号
- 数字信号处理 - 基本离散时间信号
- 数字信号处理 - 连续时间信号分类
- 数字信号处理 - 离散时间信号分类
- 数字信号处理 - 其他信号
- 基本系统特性
- 数字信号处理 - 静态系统
- 数字信号处理 - 动态系统
- 数字信号处理 - 因果系统
- 数字信号处理 - 非因果系统
- 数字信号处理 - 反因果系统
- 数字信号处理 - 线性系统
- 数字信号处理 - 非线性系统
- 数字信号处理 - 时不变系统
- 数字信号处理 - 时变系统
- 数字信号处理 - 稳定系统
- 数字信号处理 - 不稳定系统
- 数字信号处理 - 例题解析
- 数字信号处理资源
- 数字信号处理 - 快速指南
- 数字信号处理 - 有用资源
- 数字信号处理 - 讨论
数字信号处理 - 信号运算积分
任何信号的积分是指在特定时间域内对该信号进行求和,以得到一个修改后的信号。从数学上讲,这可以表示为:
$$x(t)\rightarrow y(t) = \int_{-\infty}^{t}x(t)dt$$同样,在大多数情况下,我们可以进行数学积分并找到得到的信号,但对于以矩形格式图形表示的信号,可以直接快速连续地进行积分。与微分一样,这里我们也将参考一个表格以快速获得结果。
| 原始信号 | 积分信号 |
|---|---|
| 1 | 脉冲 |
| 脉冲 | 阶跃 |
| 阶跃 | 斜坡 |
示例
让我们考虑一个信号 $x(t) = u(t)-u(t-3)$。它在下图 Fig-1 中显示。显然,我们可以看到它是一个阶跃信号。现在我们将对其进行积分。参考表格,我们知道阶跃信号的积分得到斜坡信号。
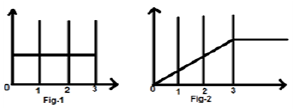
但是,我们将用数学方法计算它,
$y(t) = \int_{-\infty}^{t}x(t)dt$
$= \int_{-\infty}^{t}[u(t)-u(t-3)]dt$
$= \int_{-\infty}^{t}u(t)dt-\int_{-\infty}^{t}u(t-3)dt$
$= r(t)-r(t-3)$
同样的结果绘制在图 Fig-2 中,
广告