数字信号处理 - 时变系统

对于时变系统，输出和输入也应该延迟一段时间常数，但输入端的延迟不应该反映在输出端。所有时间尺度变换的情况都是时变系统的例子。类似地，当系统关系中的系数是时间的函数时，系统也是时变的。

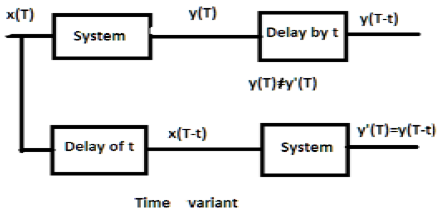
示例

a) $y(t) = x[\cos T]$

如果上述信号先通过系统再通过时间延迟，则输出将为$x\cos (T-t)$。如果它先通过时间延迟再通过系统，则输出将为$x(\cos T-t)$。由于输出不相同，因此系统是时变的。

b) $y(T) = \cos T.x(T)$

如果上述表达式先通过系统再通过时间延迟，则输出将为$\cos(T-t)x(T-t)$。但是，如果表达式先通过时间延迟再通过系统，则输出将为$\cos T.x(T-t)$。由于输出不相同，很明显系统是时变的。