Aho-Corasick算法

上一页
下一页

用于模式匹配的Aho-Corasick算法

Aho-Corasick算法是一种字典匹配算法，它可以在线性时间内找到给定文本中所有模式集的所有出现。它由Alfred V. Aho和Margaret J. Corasick于1975年开发，广泛应用于恶意软件检测、文本分析和自然语言处理等应用。

Aho-Corasick算法是如何工作的？

Aho-Corasick算法只需要遍历文本一次即可搜索所有模式，并且不会进行任何不必要的回溯。它可以轻松处理不同长度的多个关键字，也可以轻松处理重叠匹配。

该算法借助Trie数据结构跟踪已搜索的模式。Trie是一种主要用于存储字符串的树形数据结构。

让我们通过一个例子来理解：

Input:
set of patterns = {their, there, any, bye} 
main string = "isthereanyanswerokgoodbye"
Output:
Word there location: 2
Word any location: 7
Word bye location: 22
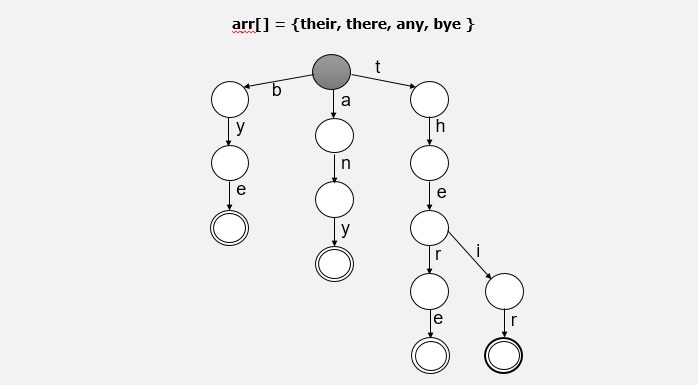
Pattern Aho-Corasick

Aho-Corasick算法包含以下步骤：

  • 预处理
  • 搜索/匹配

预处理阶段

在预处理步骤中，我们从关键字构建有限状态机（Trie）。Trie的每个节点代表关键字的一个前缀，每个可能的扩展前缀都有一条用字符标记的边。Trie的根节点代表空前缀，最后一个节点标记为最终节点。

预处理步骤进一步分为三个子步骤：

  • 跳转阶段 - 此阶段根据模式的字符定义状态之间的转换。它用二维数组表示。

  • 失败阶段 - 它定义了当发生不匹配时状态之间的转换。它用一维数组表示。

  • 输出阶段 - 在此阶段，算法存储在给定状态下结束的所有模式的索引。它也由一维数组表示。

搜索/匹配阶段

搜索步骤是通过从左到右扫描文本，并根据文本中的字符在Trie中跟随边和失败链接来完成的。每当我们到达最终节点时，我们都会报告文本中相应关键字的匹配。

示例

以下示例演示了Aho-Corasick算法在不同编程语言中的工作原理。

C C++ Java Python
#include <stdio.h>
#include <string.h>
#define MAXS 500    // sum of the length of all patterns
#define MAXC 26     // as 26 letters in alphabet
int output[MAXS];
int fail[MAXS];
int gotoMat[MAXS][MAXC];
int buildTree(char* array[], int size) {
   for(int i = 0; i<MAXS; i++)
      output[i] = 0;  // all element of output array is 0
   for(int i = 0; i<MAXS; i++)
      fail[i] = -1;  // all element of failure array is -1
   for(int i = 0; i<MAXS; i++)
      for(int j = 0; j<MAXC; j++)
         gotoMat[i][j] = -1;  // all element of goto matrix is -1
   // initial state
   int state = 1;    
   // make trie for all pattern in array
   for (int i = 0; i < size; i++) {    
      char* word = array[i];
      int presentState = 0;
      // adding pattern
      for (int j = 0; j < strlen(word); ++j) {    
         int ch = word[j] - 'a';
         if (gotoMat[presentState][ch] == -1)    
            // increasing state
            gotoMat[presentState][ch] = state++;   
         presentState = gotoMat[presentState][ch];
      }
      // adding current word in the output
      output[presentState] |= (1 << i); 
   }
   // if ch is not directly connected to root node
   for (int ch = 0; ch < MAXC; ++ch)   
      if (gotoMat[0][ch] == -1)
         gotoMat[0][ch] = 0;
   // node goes to previous state when fails
   for (int ch = 0; ch < MAXC; ++ch) {    
      if (gotoMat[0][ch] != 0) {
         fail[gotoMat[0][ch]] = 0;
         // adding next level node to the queue
         int q[MAXS], front = 0, rear = 0;
         q[rear++] = gotoMat[0][ch];
         while (front != rear) {
            // removing front node
            int state = q[front++];   
            for (int ch = 0; ch <= MAXC; ++ch) {
               // if goto state is present
               if (gotoMat[state][ch] != -1) {    
                  int failure = fail[state];
                  // find deepest node with proper suffix
                  while (gotoMat[failure][ch] == -1)    
                     failure = fail[failure];
                  failure = gotoMat[failure][ch];
                  fail[gotoMat[state][ch]] = failure;
                  // Merging output values
                  output[gotoMat[state][ch]] |= output[failure];  
                  // adding next level node to the queue
                  q[rear++] = gotoMat[state][ch];    
               }
            }
         }
      }
   }
   return state;
}
int getNextState(int presentState, char nextChar) {
   int answer = presentState;
   int ch = nextChar - 'a'; //subtract ascii of 'a'
   // if go to is not found, use failure function
   while (gotoMat[answer][ch] == -1) 
      answer = fail[answer];
   return gotoMat[answer][ch];
}
void patternSearch(char* arr[], int size, char* text) {
   buildTree(arr, size);  // make the trie structure
   int presentState = 0;  // make current state as 0
   // to find all occurances of pattern
   for (int i = 0; i < strlen(text); i++) {    
      presentState = getNextState(presentState, text[i]);
      // matching found and print words
      for (int j = 0; j < size; ++j) {  
         if (output[presentState] & (1 << j)) {
           printf("Word %s location: %zu\n", arr[j], i - strlen(arr[j]) + 1);
         }
      }
   }
}
int main() {
   char* arr[] = {"their", "there", "answer", "any", "bye"};
   char* text = "isthereanyanswerokgoodbye";
   int k = sizeof(arr)/sizeof(arr[0]);
   patternSearch(arr, k, text);
   return 0;
}

#include <iostream>
#include <queue>
#define MAXS 500    // sum of the length of all patterns
#define MAXC 26     // as 26 letters in alphabet
using namespace std;
int output[MAXS];
int fail[MAXS];
int gotoMat[MAXS][MAXC];
int buildTree(string array[], int size) {
   for(int i = 0; i<MAXS; i++)
      output[i] = 0;  // all element of output array is 0
   for(int i = 0; i<MAXS; i++)
      fail[i] = -1;  // all element of failure array is -1
   for(int i = 0; i<MAXS; i++)
      for(int j = 0; j<MAXC; j++)
         gotoMat[i][j] = -1;  // all element of goto matrix is -1
   // initial state
   int state = 1;    
   // make trie for all pattern in array
   for (int i = 0; i < size; i++) {    
      string word = array[i];
      int presentState = 0;
      // adding pattern
      for (int j = 0; j < word.size(); ++j) {    
         int ch = word[j] - 'a';
         if (gotoMat[presentState][ch] == -1)    
            // increasing state
            gotoMat[presentState][ch] = state++;   
         presentState = gotoMat[presentState][ch];
      }
      // adding current word in the output
      output[presentState] |= (1 << i); 
   }
   // if ch is not directly connected to root node
   for (int ch = 0; ch < MAXC; ++ch)   
      if (gotoMat[0][ch] == -1)
         gotoMat[0][ch] = 0;
   queue<int> q;
   // node goes to previous state when fails
   for (int ch = 0; ch < MAXC; ++ch) {    
      if (gotoMat[0][ch] != 0) {
         fail[gotoMat[0][ch]] = 0;
         q.push(gotoMat[0][ch]);
      }
   }
   while (q.size()) {
      // removing front node
      int state = q.front();   
      q.pop();
      for (int ch = 0; ch <= MAXC; ++ch) {
         // if goto state is present
         if (gotoMat[state][ch] != -1) {    
            int failure = fail[state];
            // find deepest node with proper suffix
            while (gotoMat[failure][ch] == -1)    
               failure = fail[failure];
               failure = gotoMat[failure][ch];
               fail[gotoMat[state][ch]] = failure;
               // Merging output values
               output[gotoMat[state][ch]] |= output[failure];  
               // adding next level node to the queue
               q.push(gotoMat[state][ch]);    
         }
      }
   }
   return state;
}
int getNextState(int presentState, char nextChar) {
   int answer = presentState;
   int ch = nextChar - 'a'; //subtract ascii of 'a'
   // if go to is not found, use failure function
   while (gotoMat[answer][ch] == -1) 
      answer = fail[answer];
   return gotoMat[answer][ch];
}
void patternSearch(string arr[], int size, string text) {
   buildTree(arr, size);  // make the trie structure
   int presentState = 0;  // make current state as 0
   // to find all occurances of pattern
   for (int i = 0; i < text.size(); i++) {    
      presentState = getNextState(presentState, text[i]);
      // matching found and print words
      for (int j = 0; j < size; ++j) {  
         if (output[presentState] & (1 << j)) {
            cout << "Word " << arr[j] << " location: " << i - arr[j].size() + 1 << endl;
         }
      }
   }
}
int main() {
   string arr[] = {"their", "there", "answer", "any", "bye"};
   string text = "isthereanyanswerokgoodbye";
   int k = sizeof(arr)/sizeof(arr[0]);
   patternSearch(arr, k, text);
   return 0;
}

import java.util.*;
public class Main {
   static final int MAXS = 500; // sum of the length of all patterns
   static final int MAXC = 26;  // as 26 letters in alphabet
   static int[] output = new int[MAXS];
   static int[] fail = new int[MAXS];
   static int[][] gotoMat = new int[MAXS][MAXC];
   // method to construct trie
   static int buildTree(String[] array, int size) {
      for(int i = 0; i<MAXS; i++)
         output[i] = 0;  // all element of output array is 0
      for(int i = 0; i<MAXS; i++)
         fail[i] = -1;  // all element of failure array is -1
      for(int i = 0; i<MAXS; i++)
         for(int j = 0; j<MAXC; j++)
            gotoMat[i][j] = -1;  // all element of goto matrix is -1
        // initial state
        int state = 1;    
        // make trie for all pattern in array
        for (int i = 0; i < size; i++) {    
            String word = array[i];
            int presentState = 0;
            // adding pattern
            for (int j = 0; j < word.length(); ++j) {    
                int ch = word.charAt(j) - 'a';
                if (gotoMat[presentState][ch] == -1)    
                    // increasing state
                    gotoMat[presentState][ch] = state++;   
                presentState = gotoMat[presentState][ch];
            }
            // adding current word in the output
            output[presentState] |= (1 << i); 
        }
        // if ch is not directly connected to root node
        for (int ch = 0; ch < MAXC; ++ch)   
            if (gotoMat[0][ch] == -1)
                gotoMat[0][ch] = 0;
        Queue<Integer> q = new LinkedList<>();
        // node goes to previous state when fails
        for (int ch = 0; ch < MAXC; ++ch) {    
            if (gotoMat[0][ch] != 0) {
                fail[gotoMat[0][ch]] = 0;
                q.add(gotoMat[0][ch]);
            }
        }
        while (!q.isEmpty()) {
            // removing front node
            state = q.poll();   
            for (int ch = 0; ch < MAXC; ++ch) {
                // if goto state is present
                if (gotoMat[state][ch] != -1) {    
                    int failure = fail[state];
                    // find deepest node with proper suffix
                    while (gotoMat[failure][ch] == -1)    
                        failure = fail[failure];
                    failure = gotoMat[failure][ch];
                    fail[gotoMat[state][ch]] = failure;
                    // Merging output values
                    output[gotoMat[state][ch]] |= output[failure];  
                    // adding next level node to the queue
                    q.add(gotoMat[state][ch]);    
                }
            }
        }
        return state;
    }
    static int getNextState(int presentState, char nextChar) {
        int answer = presentState;
        int ch = nextChar - 'a'; //subtract ascii of 'a'
        // if go to is not found, use failure function
        while (gotoMat[answer][ch] == -1) 
            answer = fail[answer];
        return gotoMat[answer][ch];
    }
    static void patternSearch(String[] arr, int size, String text) {
        buildTree(arr, size);  // make the trie structure
        int presentState = 0;  // make current state as 0
        // to find all occurances of pattern
        for (int i = 0; i < text.length(); i++) {    
            presentState = getNextState(presentState, text.charAt(i));
            // matching found and print words
            for (int j = 0; j < size; ++j) {  
                if ((output[presentState] & (1 << j)) != 0) {
                    System.out.println("Word " + arr[j] + " location: " + (i - arr[j].length() + 1));
                }
            }
        }
    }
    public static void main(String[] args) {
        String[] arr = {"their", "there", "answer", "any", "bye"};
        String text = "isthereanyanswerokgoodbye";
        int k = arr.length;
        patternSearch(arr, k, text);
    }
}

from collections import deque
MAXS = 500    # sum of the length of all patterns
MAXC = 26     # as 26 letters in alphabet
output = [0]*MAXS
fail = [-1]*MAXS
gotoMat = [[-1]*MAXC for _ in range(MAXS)]
# function to construct trie
def buildTree(array):
    global output, fail, gotoMat
    size = len(array)
    # initial state
    state = 1    
    # make trie for all pattern in array
    for i in range(size):    
        word = array[i]
        presentState = 0
        # adding pattern
        for j in range(len(word)):    
            ch = ord(word[j]) - ord('a')
            if gotoMat[presentState][ch] == -1:    
                # increasing state
                gotoMat[presentState][ch] = state   
                state += 1
            presentState = gotoMat[presentState][ch]
        # adding current word in the output
        output[presentState] |= (1 << i) 
    # if ch is not directly connected to root node
    for ch in range(MAXC):   
        if gotoMat[0][ch] == -1:
            gotoMat[0][ch] = 0
    q = deque()
    # node goes to previous state when fails
    for ch in range(MAXC):    
        if gotoMat[0][ch] != 0:
            fail[gotoMat[0][ch]] = 0
            q.append(gotoMat[0][ch])
    while q:
        # removing front node
        state = q.popleft()   
        for ch in range(MAXC):
            # if goto state is present
            if gotoMat[state][ch] != -1:    
                failure = fail[state]
                # find deepest node with proper suffix
                while gotoMat[failure][ch] == -1:    
                    failure = fail[failure]
                failure = gotoMat[failure][ch]
                fail[gotoMat[state][ch]] = failure
                # Merging output values
                output[gotoMat[state][ch]] |= output[failure]  
                # adding next level node to the queue
                q.append(gotoMat[state][ch])    
    return state

def getNextState(presentState, nextChar):
    answer = presentState
    ch = ord(nextChar) - ord('a') #subtract ascii of 'a'
    # if go to is not found, use failure function
    while gotoMat[answer][ch] == -1: 
        answer = fail[answer]
    return gotoMat[answer][ch]

def patternSearch(arr, text):
    buildTree(arr)  # make the trie structure
    presentState = 0  # make current state as 0
    size = len(arr)
    # to find all occurances of pattern
    for i in range(len(text)):    
        presentState = getNextState(presentState, text[i])
        # matching found and print words
        for j in range(size):  
            if (output[presentState] & (1 << j)) != 0:
                print(f"Word {arr[j]} location: {i - len(arr[j]) + 1}")

def main():
    arr = ["their", "there", "answer", "any", "bye"]
    text = "isthereanyanswerokgoodbye"
    patternSearch(arr, text)

if __name__ == "__main__":
    main()

输出

Word there location: 2
Word any location: 7
Word answer location: 10
Word bye location: 22
打印页面
上一页
下一页
广告