M着色问题

什么是M着色问题？

在M着色问题中，我们的任务是确定是否可以为给定图的节点分配m种不同的颜色，使得图中没有两个相邻的顶点具有相同的颜色。如果存在解决方案，则显示每个顶点分配了哪种颜色。M着色问题实际上用于解决诸如聚类、调度、作业分配等问题。

图是一种抽象数据类型（ADT），由一组通过链接连接的对象组成。

输入输出场景

假设给定的无向图G(V, E)及其邻接矩阵如下所示：

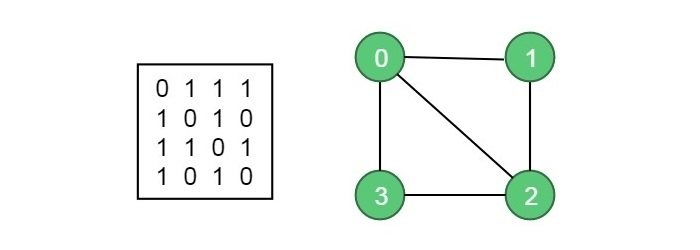
设最大颜色m = 3，表示可使用的最大颜色数。回溯算法可用于解决上述图的M着色问题。此算法将返回哪个节点将分配哪个颜色。如果解决方案不可行，则将返回false。

对于这种情况，输出应为节点0 -> 颜色1，节点1 -> 颜色2，节点2 -> 颜色3，节点3 -> 颜色2。下图说明了这一点：

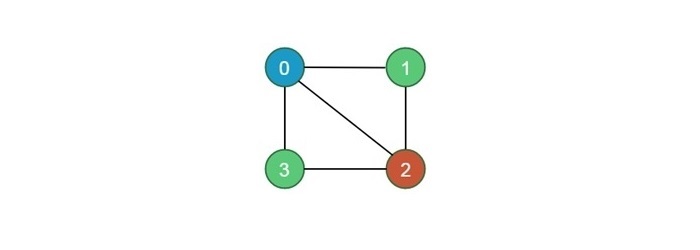
使用回溯法解决M着色问题

解决M着色问题的简单方法是生成所有可能的顶点与颜色组合，并检查是否有任何组合满足给定的约束条件。但是，对于较大的图，这种方法效率低下。

要使用回溯法解决M着色问题，请按照以下步骤操作：

从顶点0开始，我们将尝试逐个将颜色分配给不同的节点。
但是，在分配之前，我们必须检查颜色是否安全。当相邻顶点包含相同的颜色时，颜色不安全。
接下来，我们将检查是否存在任何满足约束条件的颜色分配。如果存在，我们将该分配标记为M着色问题的解决方案。

示例

在以下示例中，我们将说明如何在给定的无向图中解决M着色问题。

C C++ Java Python

Open Compiler

#include <stdio.h>
#include <stdlib.h> 
#include <stdbool.h>
#define V 4
bool graph[V][V] = {
   {0, 1, 1, 1},
   {1, 0, 1, 0},
   {1, 1, 0, 1},
   {1, 0, 1, 0}
};
void showColors(int color[]) {
   printf("Assigned Colors are:\n");
   for (int i = 0; i < V; i++)
      printf("%d ", color[i]);
   printf("\n");
}
//check whether putting a color valid for v
bool isValid(int v, int color[], int c) {
   for (int i = 0; i < V; i++)
      if (graph[v][i] && c == color[i])
         return false;
   return true;
}
bool graphColoring(int colors, int color[], int vertex) {
   //when all vertices are considered      
   if (vertex == V)
      return true;
   for (int col = 1; col <= colors; col++) {
      //check whether color is valid or not 
      if (isValid(vertex, color, col)) {
         color[vertex] = col;
         // go for additional vertices
         if (graphColoring(colors, color, vertex + 1))
            return true;
         color[vertex] = 0;
      }
   }
   //when no colors can be assigned
   return false;
}
bool checkSolution(int m) {
   //make color matrix for each vertex   
   int *color = (int *)malloc(V * sizeof(int)); 
   for (int i = 0; i < V; i++)
      //initially set to 0
      color[i] = 0;
   //for vertex 0 check graph coloring      
   if (graphColoring(m, color, 0) == false) {
      printf("Solution does not exist.\n");
      free(color); 
      return false;
   }
   showColors(color);
   free(color); 
   return true;
}

int main() {
   // Number of colors    
   int colors = 3;
   checkSolution(colors);
   return 0;
}

Open Compiler

#include<iostream>
#define V 4
using namespace std;
bool graph[V][V] = {
   {0, 1, 1, 1},
   {1, 0, 1, 0},
   {1, 1, 0, 1},
   {1, 0, 1, 0},
};
void showColors(int color[]) {
   cout << "Assigned Colors are: " <<endl;
   for (int i = 0; i < V; i++)
      cout << color[i] << " ";
   cout << endl;
}
//check whether putting a color valid for v
bool isValid(int v,int color[], int c) {    
   for (int i = 0; i < V; i++)
      if (graph[v][i] && c == color[i])
         return false;
   return true;
}
bool graphColoring(int colors, int color[], int vertex) {
   //when all vertices are considered    
   if (vertex == V)    
      return true;
   for (int col = 1; col <= colors; col++) {
      //check whether color is valid or not 
      if (isValid(vertex,color, col)) {     
         color[vertex] = col;
         // go for additional vertices
         if (graphColoring (colors, color, vertex+1) == true)    
            return true;
                   
         color[vertex] = 0;
      }
   }
   //when no colors can be assigned
   return false; 
}
bool checkSolution(int m) {
   //make color matrix for each vertex    
   int *color = new int[V];    
   for (int i = 0; i < V; i++)
      //initially set to 0
      color[i] = 0;      
   //for vertex 0 check graph coloring
   if (graphColoring(m, color, 0) == false) {    
      cout << "Solution does not exist.";
      return false;
   }
   showColors(color);
   return true;
}
int main() {
   // Number of colors    
   int colors = 3;      
   checkSolution (colors);
}

Open Compiler

public class GraphColoring {
   static final int V = 4;
   static boolean[][] graph = {
      {false, true, true, true},
      {true, false, true, false},
      {true, true, false, true},
      {true, false, true, false}
   };
   static void showColors(int[] color) {
      System.out.println("Assigned Colors are:");
      for (int i = 0; i < V; i++) {
         System.out.print(color[i] + " ");
      }
      System.out.println();
   }
   //check whether putting a color valid for v
   static boolean isValid(int v, int[] color, int c) {
      for (int i = 0; i < V; i++) {
         if (graph[v][i] && c == color[i]) {
            return false;
         }
      }
      return true;
   }
   static boolean graphColoring(int colors, int[] color, int vertex) {
      //when all vertices are considered    
      if (vertex == V) {
         return true;
      }
      for (int col = 1; col <= colors; col++) {
         //check whether color is valid or not 
         if (isValid(vertex, color, col)) {
            color[vertex] = col;
            // go for additional vertices
            if (graphColoring(colors, color, vertex + 1)) {
               return true;
            }
            color[vertex] = 0;
         }
      }
      //when no colors can be assigned
        return false;
   }
   static boolean checkSolution(int m) {
      //make color matrix for each vertex 
      int[] color = new int[V];
      for (int i = 0; i < V; i++) {
         //initially set to 0
         color[i] = 0;
      }
      //for vertex 0 check graph coloring
      if (!graphColoring(m, color, 0)) {
         System.out.println("Solution does not exist.");
         return false;
      }
      showColors(color);
      return true;
   }
   public static void main(String[] args) {
      // Number of colors 
      int colors = 3;
      checkSolution(colors);
   }
}

Open Compiler

V = 4
graph = [
    [0, 1, 1, 1],
    [1, 0, 1, 0],
    [1, 1, 0, 1],
    [1, 0, 1, 0]
]
def show_colors(color):
    print("Assigned Colors are:")
    for i in range(V):
        print(color[i], end=" ")
    print()

def is_valid(v, color, c):
    for i in range(V):
        if graph[v][i] and c == color[i]:
            return False
    return True

def graph_coloring(colors, color, vertex):
    if vertex == V:
        return True
    for col in range(1, colors + 1):
        if is_valid(vertex, color, col):
            color[vertex] = col
            if graph_coloring(colors, color, vertex + 1):
                return True
            color[vertex] = 0
    return False

def check_solution(m):
    color = [0] * V
    if not graph_coloring(m, color, 0):
        print("Solution does not exist.")
        return False
    show_colors(color)
    return True

if __name__ == "__main__":
    colors = 3
    check_solution(colors)

输出

Assigned Colors are: 
1 2 3 2

打印页面