密码系统攻击

在当今时代，不仅是商业，几乎所有人类生活方面都由信息驱动。因此，保护有用信息免受恶意活动（如攻击）的影响已变得至关重要。让我们考虑一下信息通常会受到哪些类型的攻击。

攻击通常根据攻击者执行的操作进行分类。因此，攻击可以是**被动**的或**主动**的。

被动攻击

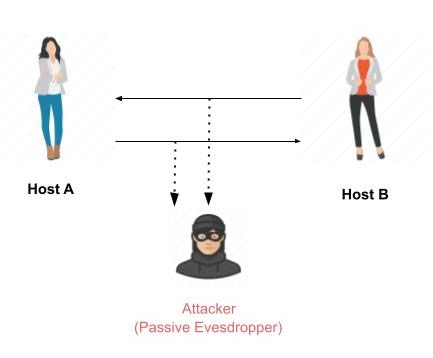
被动攻击的主要目标是**未经授权地访问信息**。例如，拦截和窃听通信通道等行为可以视为被动攻击。

这些行为本质上是被动的，因为它们既不影响信息也不破坏通信通道。被动攻击通常被视为窃取信息。窃取实物和窃取信息的区别在于，数据被盗后，所有者仍然拥有该数据。因此，被动信息攻击比窃取货物更危险，因为信息被盗可能不会被所有者注意到。

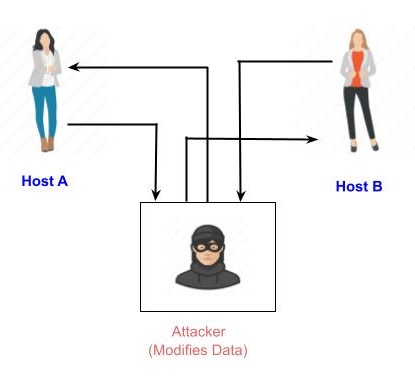
主动攻击

主动攻击涉及通过对信息进行一些处理来以某种方式更改信息。例如，

以未经授权的方式修改信息。
启动意外的或未经授权的信息传输。
更改身份验证数据，例如与信息相关的发件人名称或时间戳
未经授权删除数据。
拒绝合法用户访问信息（拒绝服务）。

密码学提供了许多工具和技术，用于实现能够防止上述大多数攻击的密码系统。

攻击者假设

让我们看看密码系统周围普遍存在的环境，然后看看用来破坏这些系统的攻击类型：

密码系统周围的环境

在考虑对密码系统的可能攻击时，了解密码系统环境是必要的。攻击者的假设和对环境的了解决定了他的能力。

在密码学中，对安全环境和攻击者的能力作出了以下三个假设。

加密方案的细节

密码系统的设计基于以下两种密码算法：

**公开算法** - 使用此选项，算法的所有详细信息都处于公共领域，每个人都知道。
**私有算法** - 算法的详细信息仅为系统设计人员和用户所知。

对于私有算法，安全性是通过模糊性来确保的。私有算法可能不是最强大的算法，因为它们是在内部开发的，并且可能没有经过广泛的弱点调查。

其次，它们只允许封闭组之间进行通信。因此，它们不适合现代通信，在现代通信中，人们与大量已知或未知的实体进行通信。此外，根据 Kerckhoff 原则，优选公开算法，加密强度取决于 *密钥*。

因此，关于安全环境的第一个假设是**攻击者知道加密算法**。

密文的可用性

我们知道，一旦明文被加密成密文，它就会被放到不安全的公共信道（例如电子邮件）上进行传输。因此，攻击者显然可以假设它**可以访问密码系统生成的密文**。

明文和密文的可用性

这个假设不像其他假设那样显而易见。但是，在某些情况下，攻击者可能**可以访问明文和对应的密文**。一些可能的这种情况是：

攻击者影响发送者转换他选择的明文并获得密文。
接收者可能无意中向攻击者泄露明文。攻击者可以访问从开放信道收集的相应密文。
在公钥密码系统中，加密密钥处于公开领域，任何潜在攻击者都知道。使用此密钥，他可以生成成对的相应明文和密文。

密码攻击

攻击者的基本意图是破坏密码系统并从密文中找到明文。为了获得明文，攻击者只需要找出秘密解密密钥，因为算法已经在公共领域。

因此，攻击者会尽最大努力找出密码系统中使用的密钥。一旦攻击者能够确定密钥，则被攻击的系统被认为是被破坏的或被入侵的。

根据使用的方法，对密码系统的攻击可分为如下几类：

仅知密文攻击 (COA) − 在这种方法中，攻击者可以访问一组密文。他无法访问相应的明文。当可以根据给定的密文集确定相应的明文时，COA 被认为是成功的。有时，可以从此攻击中确定加密密钥。现代密码系统能够抵御仅知密文攻击。
已知明文攻击 (KPA) − 在这种方法中，攻击者知道密文某些部分的明文。任务是使用此信息解密其余密文。这可以通过确定密钥或通过其他方法来完成。这种攻击的最佳示例是针对分组密码的线性密码分析。
选择明文攻击 (CPA) − 在这种方法中，攻击者可以选择要加密的文本。因此，他拥有自己选择的密文-明文对。这简化了他确定加密密钥的任务。这种攻击的一个例子是差分密码分析，它应用于分组密码和哈希函数。流行的公钥密码系统RSA也容易受到选择明文攻击。
字典攻击 − 此攻击有很多变体，所有这些变体都涉及编译“字典”。在这种攻击的最简单方法中，攻击者会构建一个包含他一段时间内学习到的密文和相应明文的字典。将来，当攻击者获得密文时，他会参考字典以查找相应的明文。
暴力攻击 (BFA) − 在这种方法中，攻击者尝试通过尝试所有可能的密钥来确定密钥。如果密钥长度为8位，则可能的密钥数量为2⁸ = 256。攻击者知道密文和算法，现在他依次尝试所有256个密钥进行解密。如果密钥很长，则完成攻击所需的时间将非常长。
生日攻击 − 此攻击是暴力技术的变体。它用于对抗密码哈希函数。当要求班上的学生说出他们的生日时，答案是365个可能的日期之一。假设第一个学生的生日是8月3日。那么，要找到下一个生日是8月3日的学生，我们需要询问大约1.25*√365 ≈ 25个学生。

同样，如果哈希函数产生64位哈希值，则可能的哈希值是1.8x10¹⁹。通过反复对不同输入评估函数，预计在大约5.1x10⁹个随机输入后将获得相同的输出。

如果攻击者能够找到两个不同的输入产生相同的哈希值，则这是一个冲突，并且该哈希函数被认为是被破坏的。
中间人攻击 (MIM) − 此攻击的目标主要是涉及密钥交换的公钥密码系统。
- 主机A想要与主机B通信，因此请求B的公钥。
- 攻击者拦截此请求并发送其公钥。
- 因此，主机A发送给主机B的任何内容，攻击者都可以读取。
- 为了保持通信，攻击者在读取后使用其公钥重新加密数据并发送给B。
- 攻击者将自己的公钥作为A的公钥发送，以便B将其视为来自A。
旁道攻击 (SCA) − 此类攻击并非针对任何特定类型的密码系统或算法。相反，它是为了利用密码系统物理实现中的弱点而发起的。
定时攻击 − 它们利用这样一个事实：不同的计算在处理器上需要不同的时间来计算。通过测量这些时间，可以了解处理器正在执行的特定计算。例如，如果加密时间更长，则表明密钥很长。
功耗分析攻击 − 这些攻击类似于定时攻击，只是使用功耗来获取有关底层计算性质的信息。
故障分析攻击 − 在这些攻击中，会在密码系统中引入错误，攻击者会研究由此产生的输出以获取有用的信息。

攻击的实用性

此处描述的对密码系统的攻击在很大程度上是学术性的，因为其中大多数来自学术界。事实上，许多学术攻击都涉及对环境以及攻击者能力的相当不现实的假设。例如，在选择密文攻击中，攻击者需要数量不切实际的故意选择的明文-密文对。这可能根本不实用。

尽管如此，任何攻击的存在都应该引起关注，特别是如果攻击技术有改进的潜力。

打印页面