密码学 - 乘法密码

在本章中，我们将深入探讨乘法密码算法及其工作原理！让我们在下面的章节中看看它。

乘法密码属于单表代换密码的范畴。在乘法密码中，明文中的每个字母都根据预先确定的乘法密钥替换为密文中相应的字母。

乘法密码背后的主要思想是使用模算术对明文进行编码和解码，模算术使用一个大的素数作为乘法密钥。在整个加密过程中，明文中每个字母的数值都乘以密钥，然后计算结果对密钥取模。例如，如果明文字母是“s”并且密钥是 7，则密文字母是 (18*7) mod 26 = 22，因为“s”的数值是 18。因此，在这种情况下，字母“a”的密文符号将是“w”。

解密只是反向执行加密过程：密文中每个字母都赋予一个数值，该数值除以密钥，然后结果对密钥取模。乘法密码的一个主要优点是它的简单性——即易于实现、理解和处理能力要求低。

但是这种方法虽然易于使用和理解，但安全性不高。它类似于一个简单的秘密代码，很容易被别人破解。对于小事情来说，它是合适的，但对于需要强力保护的重要事情来说，它是不合适的。

乘法密码是如何工作的？

你的密钥是一个你选择的大的素数。然后你使用数学运算修改消息中的每个字母。例如，如果你的密钥是 7，并且你的消息包含字母“s”，它是数字 18，你执行 (18 乘以 7) 除以 26 并取余数。这将给你 22，它对应于字母“w”。因此，“s”在秘密消息中变为“w”。

你只需反转数学运算即可读取秘密消息。你可以用密钥除以每个字母的数字，并取余数。

如果使用乘法转换为密文，则称为环绕情况。请考虑如下所示的字母和关联的数字−

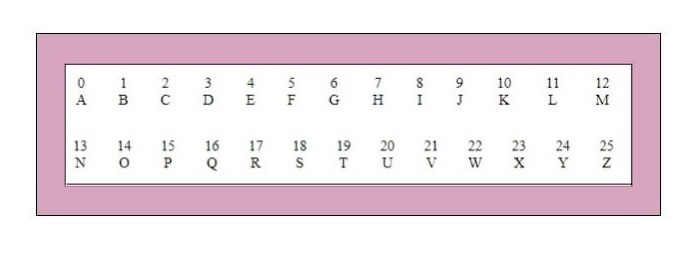
这些数字将被乘以，相应的密钥是 7。在这种情况下，要创建乘法密码，基本公式如下−

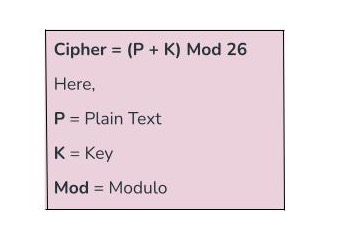
现在使用上述公式将“hello”转换为密文，使用密钥 K。假设我们的密钥 K 是 3。以下是我们将如何将给定公式应用于“hello”中的每个字母−

对于“h”：P（“h”的明文值）= 7（假设“a”是 0，“b”是 1，…，“h”是 7）

密文 = (7 + 3) Mod 26 = 10 Mod 26 = 10

对于“e”：P（“e”的明文值）= 4

密文 = (4 + 3) Mod 26 = 7 Mod 26 = 7

对于“l”：P（“l”的明文值）= 11

密文 = (11 + 3) Mod 26 = 14 Mod 26 = 14

对于“l”：P（“l”的明文值）= 11

密文 = (11 + 3) Mod 26 = 14 Mod 26 = 14

对于“o”：P（“o”的明文值）= 14

密文 = (14 + 3) Mod 26 = 17 Mod 26 = 17

因此，关于数字 10、7、14、14、17 的值分别是 k、h、o、o、r。

因此，密钥为 3 的“hello”的密文将是“khoor”。

乘法密码算法

加密算法

• 首先，你需要选择一个素数作为加密密钥。

• 为明文消息中的每个字母分配数值。

• 将每个数值乘以加密密钥。

• 取结果模 26，即英语字母表中字母的数量，以确保结果应保持在字母表的范围内。

• 将结果数值转换回字母以获取密文消息。

解密算法

• 选择与解密密钥相同的素数。

• 为密文消息中的每个字母分配数值。

• 将每个数值除以解密密钥。

• 取结果模 26。

• 将结果数值转换回字母以获取原始明文消息。

使用 Python 实现

因此，我们可以通过不同的方式实现此算法−

使用基本算术

在本例中，我们将使用基本的算术运算来进行乘法密码的加密和解密。因此，在加密过程中，我们将使用ASCII值将明文消息转换为数字（0-25）。每个数字将乘以加密密钥。然后，对结果取模26，以确保它落在字母范围（0-25）内。最后，我们将使用ASCII值将数字转换回字符。

在解密过程中，我们将使用ASCII值将密文消息转换为数字（0-25）。每个数字乘以加密密钥的模逆元。然后对结果取模26。最后，将得到的数字使用ASCII值转换回字符。

示例

下面是乘法密码算法的简单Python代码。请查看下面的程序 -

def multiplicative_encrypt(message, key):
   cipher_text = ''
   for char in message:
      if char.isalpha():
         # Change char to number (0-25)
         num = ord(char.lower()) - ord('a')
         # Encrypt with the help of (P * K) % 26
         encrypted_num = (num * key) % 26
         # change back to character
         cipher_text += chr(encrypted_num + ord('a'))
      else:
         cipher_text += char
   return cipher_text

def multiplicative_decrypt(ciphertext, key):
   plain_text = ''
   # get the modular multiplicative inverse of the key
   inverse_key = pow(key, -1, 26)
   for char in ciphertext:
      if char.isalpha():
         # change char to number (0-25)
         num = ord(char.lower()) - ord('a')
         # Decrypt using the formula (C * K_inverse) % 26
         decrypted_num = (num * inverse_key) % 26
         # change back to character
         plain_text += chr(decrypted_num + ord('a'))
      else:
         plain_text += char
   return plain_text

plaintext = "hello tutorialspoint"
key = 7
encrypted_message = multiplicative_encrypt(plaintext, key)
print("Encrypted message:", encrypted_message)
decrypted_message = multiplicative_decrypt(encrypted_message, key)
print("Decrypted message:", decrypted_message)

以下是上述示例的输出 -

输入/输出

Encrypted message: xczzu dkdupeazwbuend
Decrypted message: hello tutorialspoint

使用sympy和math库

在下面的示例中，我们将使用Python的sympy和math库来实现不同的目的 -

Sympy库 - 从sympy库中，我们将导入mod_inverse函数。此函数将用于计算一个数的模逆元。在乘法密码中，此函数用于查找加密/解密密钥模26的逆元。

Math库 - 我们将导入整个math库。我们将使用math库中的math.gcd()函数来计算26和加密/解密密钥的最大公约数（GCD）。GCD用于检查密钥是否与26互质。此检查对于确保密钥对加密有效非常重要。

简单来说，我们可以说sympy库用于计算模逆元，而math库用于计算密钥验证的最大公约数。这两个库都提供了在实现乘法密码算法中很有用的数学函数。

示例

以下是乘法密码算法的简单Python代码。请查看下面的代码 -

from sympy import mod_inverse
import math

def multiplicative_cipher(text, mode, key):
   char_to_num = {}
   result_message = ''

   # dictionary mapping characters to their numerical values
   for i in range(26):
      char_to_num[chr(ord('a') + i)] = i

   # List of characters
   char_list = list(char_to_num.keys())

   # Dictionary mapping numerical values to characters
   num_to_char = dict(zip(char_to_num.values(), char_to_num.keys()))

   if mode == 'encrypt':
      if math.gcd(26, key) == 1:
         # Encryption
         for char in text:
            if char in char_list:
               # Encrypt each character
               new_num = (char_to_num[char] * key) % 26
               result_message += num_to_char[new_num]
            else:
               # Leave non-alphabetic characters unchanged
               result_message += char
      else:
            print('Invalid key selected')
        
   elif mode == 'decrypt':
      # Calculate the multiplicative inverse of the key
      inv_key = mod_inverse(key, 26)
      # Decryption
      for char in text:
         if char in char_list:
            # Decrypt each character
            new_num = (char_to_num[char] * inv_key) % 26
            result_message += num_to_char[new_num]
         else:
            # Leave non-alphabetic characters unchanged
            result_message += char
    
   return result_message
  
encrypted_text = multiplicative_cipher('hello world', 'encrypt', 7)
print("Encrypted message:", encrypted_text)
decrypted_text = multiplicative_cipher('xczzu yupzv', 'decrypt', 7)
print("Decrypted message:", decrypted_text)

以下是上述示例的输出 -

输入/输出

Encrypted message: xczzu yupzv
Decrypted message: hello world

使用Java实现

现在，我们将使用Java编程语言创建一个乘法密码程序。其中，我们将有一个类，以及两个函数，通过它们我们可以加密和解密给定的明文消息。

示例

因此，使用Java编程语言的实现如下 -

public class MultiplicativeCipher {
   private int key;

   public MultiplicativeCipher(int k) {
      key = k;
   }

   public String encrypt(String plaintext) {
      StringBuilder ciphertext = new StringBuilder();
      for (char c : plaintext.toCharArray()) {
         if (Character.isLetter(c)) {
            if (Character.isUpperCase(c))
               ciphertext.append((char)(((c - 'A') * key) % 26 + 'A'));
            else
               ciphertext.append((char)(((c - 'a') * key) % 26 + 'a'));
         } else {
            ciphertext.append(c);
         }
      }
      return ciphertext.toString();
   }

   public String decrypt(String ciphertext) {
      StringBuilder plaintext = new StringBuilder();
      int modInverse = 0;
      for (int i = 0; i < 26; i++) {
         if ((key * i) % 26 == 1) {
            modInverse = i;
            break;
         }
      }
      for (char c : ciphertext.toCharArray()) {
         if (Character.isLetter(c)) {
            if (Character.isUpperCase(c))
               plaintext.append((char)(((c - 'A') * modInverse) % 26 + 'A'));
            else
               plaintext.append((char)(((c - 'a') * modInverse) % 26 + 'a'));
         } else {
            plaintext.append(c);
         }
      }
      return plaintext.toString();
   }

   public static void main(String[] args) {
      MultiplicativeCipher cipher = new MultiplicativeCipher(3); // Set the key to 3
      String plaintext = "Hello world, How are you";
      String ciphertext = cipher.encrypt(plaintext);
      System.out.println("The Encrypted text: " + ciphertext);
      System.out.println("The Decrypted text: " + cipher.decrypt(ciphertext));
   }
}

以下是上述示例的输出 -

输入/输出

The Encrypted text: Vmhhq oqzhj, Vqo azm uqi
The Decrypted text: Hello world, How are you

使用C++实现

我们将使用C++编程语言来实现乘法密码。我们将有一个名为MultiplicativeCipher的类。它提供了消息加密和解密的工具。encrypt()方法将使用提供的密钥加密输入的文本字符串并返回结果。而decrypt()方法将使用给定的密钥解密密文字符串并返回明文。

示例

因此，使用C++实现乘法密码如下 -

#include <iostream>
#include <string>

using namespace std;

class MultiplicativeCipher {
private:
   int key;

public:
   MultiplicativeCipher(int k) {
      key = k;
   }

   string encrypt(string plaintext) {
      string ciphertext = "";
      for (char& c : plaintext) {
         if (isalpha(c)) {
            if (isupper(c))
               ciphertext += char(((c - 'A') * key) % 26 + 'A');
            else
               ciphertext += char(((c - 'a') * key) % 26 + 'a');
         } else {
            ciphertext += c;
         }
      }
      return ciphertext;
   }

   string decrypt(string ciphertext) {
      string plaintext = "";
      int modInverse = 0;
      for (int i = 0; i < 26; i++) {
         if ((key * i) % 26 == 1) {
            modInverse = i;
            break;
         }
      }
      for (char& c : ciphertext) {
         if (isalpha(c)) {
            if (isupper(c))
               plaintext += char(((c - 'A') * modInverse) % 26 + 'A');
            else
               plaintext += char(((c - 'a') * modInverse) % 26 + 'a');
         } else {
            plaintext += c;
         }
      }
      return plaintext;
   }
};

int main() {
   MultiplicativeCipher cipher(3); // Set the key to 3
   string plaintext = "hello this world is awesome!";
   string ciphertext = cipher.encrypt(plaintext);
   cout << "The Encrypted text: " << ciphertext << endl;
   cout << "The Decrypted text: " << cipher.decrypt(ciphertext) << endl;
   return 0;
}

以下是上述示例的输出 -

输入/输出

The Encrypted text: vmhhq fvyc oqzhj yc aomcqkm!
The Decrypted text: hello this world is awesome!

乘法密码的特征

以下是乘法密码的一些主要特征 -

• 乘法密码易于理解和使用。它遵循一种简单的替换消息中字母的方法。

• 它依赖于素数作为加密和解密的密钥。

• 该密码使用模运算，其中我们在除法后取余数。此方法帮助我们将加密值保持在一定范围内，在乘法密码的情况下，它是字母表的长度。

• 由于它非常易于实现，因此不适用于传输敏感信息。它可以使用基本技术轻松破解。

• 它不需要大量的计算能力来加密或解密消息。

• 乘法密码适用于小型应用或安全要求不高的场景。

总结

在本章中，我们学习了乘法密码及其实现。乘法密码是一种将消息转换为秘密代码的方法，方法是使用乘以一个特殊数字（称为密钥）的方式替换每个字母。有不同的方法来实现这种密码技术，我们使用了不同的编程语言，例如Python、C++和Java。您可以使用基本的算术运算或sympy和math之类的库。代码示例展示了如何使用这些方法加密和解密消息。您可以根据您的理解和使用情况使用它们。