
- 密码学教程
- 密码学 - 首页
- 密码学 - 起源
- 密码学 - 历史
- 密码学 - 原理
- 密码学 - 应用
- 密码学 - 优点与缺点
- 密码学 - 现代
- 密码学 - 传统密码
- 密码学 - 加密的需求
- 密码学 - 双重强度加密
- 密码系统
- 密码系统
- 密码系统 - 组件
- 密码系统攻击
- 密码系统 - 彩虹表攻击
- 密码系统 - 字典攻击
- 密码系统 - 暴力攻击
- 密码系统 - 密码分析技术
- 密码学类型
- 密码系统 - 类型
- 公钥加密
- 现代对称密钥加密
- 密码学哈希函数
- 密钥管理
- 密码系统 - 密钥生成
- 密码系统 - 密钥存储
- 密码系统 - 密钥分发
- 密码系统 - 密钥撤销
- 分组密码
- 密码系统 - 流密码
- 密码学 - 分组密码
- 密码学 - Feistel 分组密码
- 分组密码的工作模式
- 分组密码的工作模式
- 电子密码本 (ECB) 模式
- 密码分组链接 (CBC) 模式
- 密码反馈 (CFB) 模式
- 输出反馈 (OFB) 模式
- 计数器 (CTR) 模式
- 经典密码
- 密码学 - 逆向密码
- 密码学 - 凯撒密码
- 密码学 - ROT13 算法
- 密码学 - 换位密码
- 密码学 - 加密换位密码
- 密码学 - 解密换位密码
- 密码学 - 乘法密码
- 密码学 - 仿射密码
- 密码学 - 简单替换密码
- 密码学 - 简单替换密码的加密
- 密码学 - 简单替换密码的解密
- 密码学 - 维吉尼亚密码
- 密码学 - 维吉尼亚密码的实现
- 现代密码
- Base64 编码和解码
- 密码学 - XOR 加密
- 替换技术
- 密码学 - 单字母替换密码
- 密码学 - 单字母替换密码的破解
- 密码学 - 多字母替换密码
- 密码学 - Playfair 密码
- 密码学 - Hill 密码
- 多字母替换密码
- 密码学 - 一次性密码本密码
- 一次性密码本密码的实现
- 密码学 - 换位技术
- 密码学 - 栅栏密码
- 密码学 - 列置换
- 密码学 - 隐写术
- 对称算法
- 密码学 - 数据加密
- 密码学 - 加密算法
- 密码学 - 数据加密标准
- 密码学 - 三重DES
- 密码学 - 双重DES
- 高级加密标准
- 密码学 - AES 结构
- 密码学 - AES 变换函数
- 密码学 - 字节替换变换
- 密码学 - 行移位变换
- 密码学 - 列混合变换
- 密码学 - 轮密钥加变换
- 密码学 - AES 密钥扩展算法
- 密码学 - Blowfish 算法
- 密码学 - SHA 算法
- 密码学 - RC4 算法
- 密码学 - Camellia 加密算法
- 密码学 - ChaCha20 加密算法
- 密码学 - CAST5 加密算法
- 密码学 - SEED 加密算法
- 密码学 - SM4 加密算法
- IDEA - 国际数据加密算法
- 公钥(非对称)密码学算法
- 密码学 - RSA 算法
- 密码学 - RSA 加密
- 密码学 - RSA 解密
- 密码学 - 创建 RSA 密钥
- 密码学 - 破解 RSA 密码
- 密码学 - ECDSA 算法
- 密码学 - DSA 算法
- 密码学 - Diffie-Hellman 算法
- 密码学中的数据完整性
- 密码学中的数据完整性
- 消息认证
- 密码学数字签名
- 公钥基础设施
- 哈希
- MD5(消息摘要算法 5)
- SHA-1(安全哈希算法 1)
- SHA-256(安全哈希算法 256 位)
- SHA-512(安全哈希算法 512 位)
- SHA-3(安全哈希算法 3)
- 哈希密码
- Bcrypt 哈希模块
- 现代密码学
- 量子密码学
- 后量子密码学
- 密码学协议
- 密码学 - SSL/TLS 协议
- 密码学 - SSH 协议
- 密码学 - IPsec 协议
- 密码学 - PGP 协议
- 图像和文件加密
- 密码学 - 图像
- 密码学 - 文件
- 隐写术 - 图像
- 文件加密和解密
- 密码学 - 文件加密
- 密码学 - 文件解密
- 物联网中的密码学
- 物联网安全挑战、威胁和攻击
- 物联网安全的加密技术
- 物联网设备的通信协议
- 常用的加密技术
- 自定义构建加密算法(混合加密)
- 云加密
- 量子密码学
- 密码学中的图像隐写术
- DNA 密码学
- 密码学中的一次性密码 (OTP) 算法
- 区别
- 密码学 - MD5 与 SHA1
- 密码学 - RSA 与 DSA
- 密码学 - RSA 与 Diffie-Hellman
- 密码学与密码学
- 密码学 - 密码学与密码分析
- 密码学 - 经典与量子
- 密码学与隐写术
- 密码学与加密
- 密码学与网络安全
- 密码学 - 流密码与分组密码
- 密码学 - AES 与 DES 密码
- 密码学 - 对称与非对称
- 密码学有用资源
- 密码学 - 快速指南
- 密码学 - 讨论
密码系统 - 概述
密码系统使用密码方法及其周围的支持结构来保护信息。它也称为密码系统。
密码系统使用算法将明文转换为密文,以安全地编码或解码消息。术语密码系统指的是一个使用密码的计算机系统,代码用于保护信息和通信,以便只有预期的人员才能阅读和处理它。
密码系统使用密钥创建、加密和解码算法来确保数据安全。加密密钥(算法使用的比特串)将明文转换为编码文本,反之亦然。
密钥和可变数据作为输入提供给算法以执行此操作。算法的安全性依赖于安全的密钥。
密码系统在线安全地使用信用卡等私人数据。安全电子邮件使用签名、哈希和密钥管理。
我们将研究一个基本的密码系统模型。此模型使传输的信息保密。您可以在下面的图片中看到这个简单的模型 -
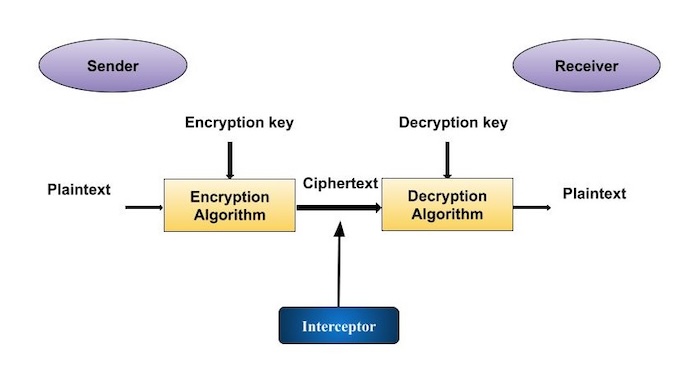
上图显示了发送方以一种无法被通信通道中的任何经过身份验证的第三方或第三方提取数据的方式向接收方传输敏感信息。
这个简单加密方案的目标是,在流程结束时,只有发送方和接收方才能知道私人信息。
加密密钥
密钥在作为输入提交给加密算法的可变信息中起着重要作用,以执行加密或解密过程。密码系统的安全性在很大程度上取决于所用密钥的安全性。如果未经授权的方能够访问密钥,他们可能会解密加密的消息,假装成其他人,或加密误导性的消息以冒充他人。必须将密钥保密并安全地生成、分发和存储,以维护密码系统的完整性。加密的强度也取决于密钥的长度和复杂性。
密码系统类型
从根本上说,根据系统中执行加密-解密的方式,密码系统有两种类型 -
对称密钥加密
非对称密钥加密
这些密码系统之间最大的区别在于加密和解密密钥之间的链接。在任何密码系统中,这两个密钥在逻辑上都是相关的。使用与加密密钥无关的密钥几乎不可能解密密文。
对称密钥加密
使用相同的密钥对信息进行加密和解密的加密过程称为对称密钥加密。
对称密码系统的研究称为对称密码学。对称密码系统有时也称为秘密密钥密码系统。
一些众所周知的对称密钥加密方法的例子包括 - 数据加密标准 (DES)、三重 DES (3DES)、IDEA 和 BLOWFISH。
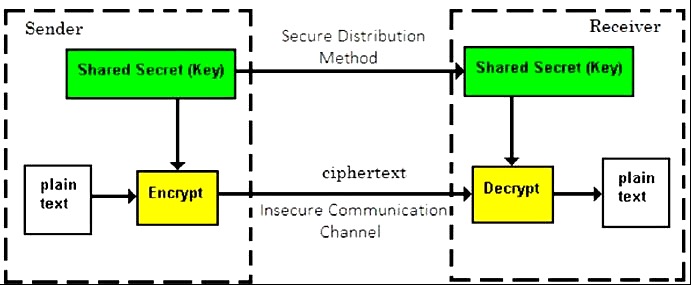
在 1970 年之前,所有密码系统都使用对称密钥加密。即使在今天,它的相关性也非常高,并且已广泛应用于许多密码系统中。这种加密不太可能消失,因为它比非对称密钥加密具有一定的优势。
基于对称密钥加密的密码系统的显著特征是 -
使用对称密钥加密的人员必须在交换信息之前共享一个通用密钥。
建议定期更改密钥以防止对系统进行任何攻击。
需要一个强大的机制来在通信双方之间交换密钥。由于需要定期更改密钥,因此此技术变得昂贵且繁琐。
在一个由 n 个人组成的小组中,为了使任何两个人之间都能进行双向通信,该小组所需的密钥数量为 n x (n − 1)/2。
此加密中密钥的长度(位数)较小,因此加密-解密过程比非对称密钥加密快。
运行对称算法所需的计算机系统的处理能力较低。
对称密钥密码系统的挑战
使用对称密钥密码学有两个主要挑战。
密钥建立 - 在任何通信之前,发送方和接收方都需要就一个秘密的对称密钥达成一致。它需要一个安全的密钥管理方案。
信任问题 - 由于发送方和接收方使用相同的对称密钥,因此隐含地要求发送方和接收方“相互信任”。例如,可能会发生接收方将密钥丢失给攻击者,而发送方没有被告知的情况。
这两个挑战对于现代通信来说具有很大的限制性。如今,人们需要与不熟悉且不可信的各方交换信息。例如,在线卖家和客户之间的沟通。对称密钥加密的这些限制催生了非对称密钥加密方案。
非对称(公钥)加密
非对称密钥加密是使用各种密钥对信息进行加密和解密的过程。尽管密钥不同,但它们在数学上是相似的,因此可以通过解密密文来获取明文。该过程在以下插图中描述 -
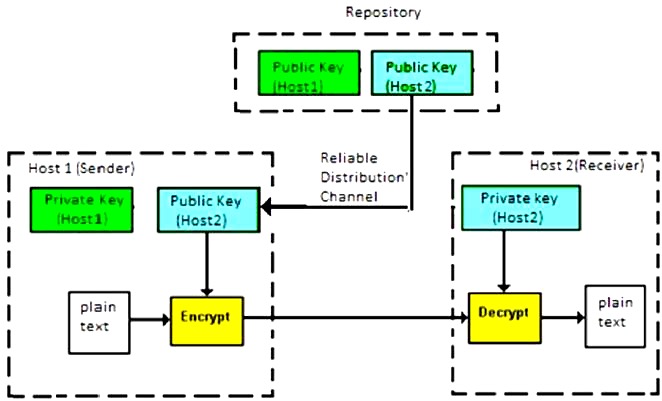
非对称密钥加密算法诞生于20世纪,旨在解决通信双方需要预先共享密钥的问题。该加密方案的主要特点如下:
系统中的每个用户都需要拥有一个由私钥和公钥组成的密钥对。由于这两个密钥之间存在数学关系,因此无论使用哪一个密钥进行加密,都可以解密密文并恢复原始明文。
公钥需要存储在公共存储库中,而私钥则需要严格保密。因此,这种加密方案也被称为公钥加密。
尽管用户的公钥和私钥之间存在关联,但从一个密钥推导出另一个密钥在计算上是不可行的。这是该方案的优势所在。
当主机1需要向主机2发送数据时,它会从存储库中获取主机2的公钥,对文件进行加密,然后发送。
主机2使用其私钥解密文件,提取明文。
这种加密算法的密钥长度(比特数)较长,因此加密和解密过程比对称密钥加密慢。
运行非对称算法所需的计算机系统处理能力较高。
对称加密系统是一个比较直观的概念。相比之下,公钥加密系统则比较难以理解。
你可能会想,加密密钥和解密密钥是如何“相关”的,同时又不可能从加密密钥推导出解密密钥呢?答案在于数学原理。可以创建一种密钥具备此特性的加密系统。公钥密码学的概念相对较新。已知的公钥算法比对称算法少。
公钥加密系统的挑战
公钥加密系统的一个基本问题是,用户必须相信他在与另一个人通信时使用的公钥确实是该人的公钥,而不是由第三方创建的。
这通常是通过一个由可信第三方组成的公钥基础设施(PKI)来实现的。第三方安全地管理和认证公钥的真实性。当第三方被要求提供任何通信者X的公钥时,人们相信他们会提供正确的公钥。
第三方通过授权、签名或其他程序来确保用户身份,即X是唯一且全球唯一的X。提供已验证公钥的最常见方法是将它们嵌入到由可信第三方数字签名的证书中。
加密方案之间的关系
下面总结了两种类型的加密系统的基本密钥特性:
| 标题 | 密钥之间的关系 | 加密密钥 | 解密密钥 |
|---|---|---|---|
| 对称加密系统 | 相同 | 对称 | 对称 |
| 公钥加密系统 | 不同,但存在数学关系 | 公钥 | 私钥 |
由于两种系统都各有优缺点,因此在实际的信息安全系统中,通常将对称密钥加密和公钥加密系统结合使用。
柯克霍夫原则
柯克霍夫原则是在加密领域的一个重要概念。它认为,加密系统的强度不应该依赖于保持加密方法的秘密。相反,安全性应该来自保护加密密钥。即使加密过程的细节成为公开知识,一个设计良好的加密系统也需要保持安全。
这个理念对于现代加密标准至关重要——它促进了算法设计和分析的透明度。只要密钥被隐藏,就可以公开加密过程的具体细节。这鼓励安全专家共同审查加密方法。这也意味着可以公开提出和测试新的算法,并确信它们不会仅仅因为发布而被破解。最终,柯克霍夫原则之所以具有基础性,是因为它将重点转移到勤勉地保护加密触发器上,而不是徒劳地试图隐藏加密机制本身。
通过密码学实现信息安全的概念起源于19世纪后期。它最初是由荷兰密码学家奥古斯特·柯克霍夫提出的,他为现代密码分析和安全加密系统的设计奠定了基础。后来在20世纪,美国数学家和密码学家克劳德·香农进一步发展了密码学和安全理论。
柯克霍夫为密码系统定义的六项设计原则如下:
密码系统应该在实践上,如果不是在数学上,是不可破解的。
密码系统落入入侵者手中不应导致任何系统妥协,防止给用户带来任何不便。
密钥应该易于沟通、记忆和更改。
密文应该可以通过电报(一个不安全的信道)传输。
加密设备和文档应该是便携的,可以由一个人操作。
最后,系统必须易于使用,既不需要精神上的压力,也不需要了解一套冗长的规则。
第二条规则目前被称为柯克霍夫原则。它几乎应用于所有现代加密算法,例如DES、AES等。这些公开的算法被认为是完全安全的。加密消息的安全性完全取决于密钥的安全性。
保持算法的秘密可能会成为密码分析的一个重大障碍。但是,只有在严格限制的范围内使用算法时,才能保持算法的秘密。
密码系统的重要性
密码系统在保护通过互联网发送的敏感信息方面发挥着重要作用。它们允许用户以安全的方式传输私人数据,例如信用卡号码。密码学在除了消息传递之外的各种应用中都有广泛用途。例如,安全的电子邮件系统可以包含数字签名以验证发件人的身份。它还可以使用密码散列函数来验证消息在传输过程中是否被篡改。此外,此类系统将管理加密密钥以加密和解密通信。总的来说,密码学技术有助于确保数字通信的隐私和完整性。