IDEA - 国际数据加密算法

IDEA代表国际数据加密算法。IDEA是由James Massey和Xuejia Lai开发的一种分组密码，最初于1991年制定。它具有128位的密钥长度，并使用64位的块进行操作。

它由一组八个相同的变换组成，这些变换基于按位异或、加法和乘法模块。它基于对称密码，并使用相对较弱的密钥设计技术，因此该算法的安全性远低于DES。由于其复杂的开发过程，IDEA未能获得广泛的普及。

IDEA不同于其他分组密码算法，它正在被瑞士公司Ascom研究。然而，他们的独特之处在于他们允许免费的非商业用途，这使得IDEA成为著名的消息字符加密中使用的分组密码算法。

IDEA的工作原理？

IDEA是一种分组密码，它对64位明文和128位密钥进行操作。与DES一样，IDEA是可逆的，这意味着相同的技术可用于加密和解密。IDEA需要扩散和混淆来进行加密。

64位明文被分成四个16位的部分（P1-P4）。这些是第一轮的输入。共有八轮这样的操作。密钥包含128位。在每个循环中，从原始密钥生成六个子密钥，每个子密钥包含16位。

第一轮可以使用密钥K1到K6，第二轮可以使用密钥K7到K12，最后一轮可以使用密钥K13到K18。最后一步需要一个输出修改，需要四个子密钥（K49到K52）。

最终输出是输出变换阶段的结果。块C1-C4连接起来生成最终结果。

IDEA中的轮次

IDEA共有八轮。每一轮都包括对四个数据块和六个密钥的一系列操作。第一轮可以包含密钥K1到K6，第二轮可以包含密钥K7到K12，最后一轮可以包含密钥K13到K18。最后阶段涉及一个输出修改，需要四个子密钥（K49到K52）。

最终输出是输出变换阶段的结果。最终输出是通过连接块C1-C4形成的。每一轮有14个步骤，如下所示：

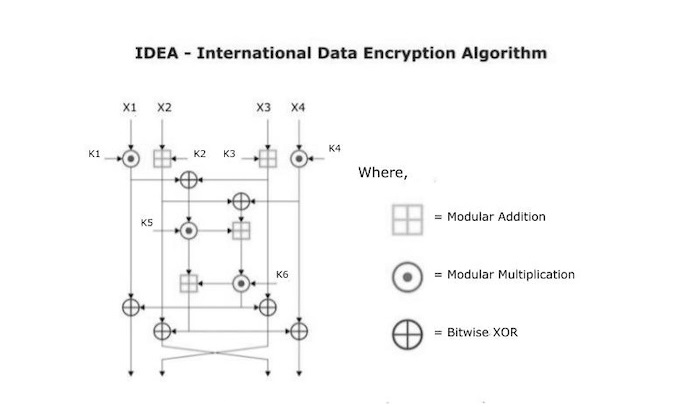
IDEA中一轮的细节

Step1  : Multiply * P1 and K1
Step2  : Add * P2and K2
Step3  : Add * P3and K3
Step4  : Multiply * P4 and K4
Step5  : XOR the results of step1 and step3
Step6  : XOR the results of step2 and step4
Step7  : Multiply * the results of step5 with K5
Step8  : Add * the results of step6 and step7
Step9  : Multiply * the results of step8 with K6
Step10 : Add * the results of step7 and step9
Step11 : XOR the results of step1 and step9
Step12 : XOR the results of step3 and step9
Step13 : XOR the results of step2 and step10
Step14 : XOR the results of step4 and step10

在每个循环中的下一步中，“加法*”和“乘法*”不是基本的加法和乘法，而是模2¹⁶（模65536）加法和模2¹⁶+1（模65537）乘法。输入和输出都是无符号的16位整数。

普通的加法会得到一个17位的数字。它只能使用16位空间用于round2输出。

因此，它可以将这个数字（十进制为130753）减少到一个16位的数值。它可以取这个数模65536。130753模65536得到65217，其二进制表示为11111111011000001，是一个很好的16位整数。

输入块为P1-P4，子密钥为K1-K6，此步骤的输出为R1-R4（而不是C1-C4，因为这不是最终的密文）。这是一个中间输出，将在后续步骤以及输出变换阶段处理。

IDEA中使用的操作

IDEA的操作包括：

IDEA使用按位异或，表示为⊕
模2¹⁶（模65536）整数加法，使用无符号16位整数作为输入和输出。
此操作称为⊕。
模2¹⁶+1（模65537）整数乘法，输入和输出都是无符号的16位整数。全零块表示2¹⁶。此操作称为⊗。

一轮的子密钥生成

在第一轮中，使用密钥的第1-96位。第97-128位保持未使用。它们被分配到第二轮。
在第二轮中，首先使用第97-128位，进行25位的循环左移，然后使用新的第26-89位。第90-128位和第1-25位保持未使用。
在第三轮中，再次使用未使用的第90-128位和第1-25位，然后进行25位的循环左移，并使用第51-82位。第83-128位和第1-50位保持未使用。
在第四轮中，使用第83-128位和第1-50位。
在第五轮中，发生25位的循环左移，使用第76-128位和第1-43位。第44-75位保持未使用。
在第六轮中，使用第五轮中未使用的位，并进行25位的循环左移，留下第37-100位未使用。
在第七轮中，首先使用第六轮中未使用的位，第37-100位，然后进行25位的循环左移到第126-128位和第1-29位。第30-125位保持未使用。
使用第七轮中未使用的位，第30-125位，密钥被停用。

输出变换

这是一个一次性操作。它发生在第八轮结束时。因此，一个64位的数值被分成四个子块（例如R1到R4），每个子块都有自己的子密钥。

解密

解密类似于加密，但是它反转轮密钥和奇数轮的子密钥的顺序。因此，K49-K52的逆反恢复了相应密码学集合操作中子密钥K1-K4的值，而每组的K5和K6应该由K47和K48恢复以进行此密码学操作中的解密。

IDEA的特性

以下特性与IDEA的密码强度有关：

分组长度 − 分组长度应防止统计分析。然而，开发有效加密算法的复杂性似乎随着分组大小呈指数增长。
密钥强度 − 密钥长度应足够长，以避免穷举密钥搜索。IDEA 使用 128 位密钥长度，在未来相当长一段时间内在这个方面似乎都是安全的。
混淆 − 密文应以复杂且有效的方式依赖于明文和密钥。目标是使确定密文统计与明文统计之间关系变得更加困难。IDEA 通过随后讨论的三个不同的操作来实现此目的。这与主要基于 XOR 运算和小型非线性 S 盒的 DES 形成对比。
扩散 − 每个明文位都应影响每个密文位，就像每个密钥位都应影响每个密文位一样。单个明文位在多个密文位上的分散模糊了明文的统计结构。IDEA 在这方面非常有效。

IDEA 的安全性

IDEA 加密方法被认为对某些类型的攻击（例如差分密码分析）非常强大。直到 2007 年，没有人成功发现其设计中的弱点。即使是当时已知的最佳攻击也只能破解简化版（6 轮）的 IDEA，而完整版使用 8.5 轮。

受人尊敬的密码学家布鲁斯·施奈尔 (Bruce Schneier) 在 1996 年称赞 IDEA 是当时最好、最安全的加密方法。然而，到 1999 年，他停止推荐它，因为开发出了更新、更快的算法，在 IDEA 中发现了一些弱点，并且存在专利问题。

2011 年，一种名为“中间相遇”的方法被用来破解完整的 8.5 轮 IDEA 加密。然后，在 2012 年，另一种名为“窄双向群”的攻击被用来稍微削弱 IDEA，但它对于实际使用仍然安全。

打印页面