密码学 - ECDSA 算法

上一页
下一页

椭圆曲线数字签名算法 (ECDSA) 是最复杂的公钥密码加密技术之一。椭圆曲线密码学生成的密钥比数字签名方法生成的密钥更小。一种称为椭圆曲线密码学的公钥加密利用了有限域上椭圆曲线的代数结构。

椭圆曲线密码学主要用于创建伪随机数和数字签名等。数字签名是一种身份验证机制，它使用公钥对和数字证书来验证信息接收者或发送者的身份。

什么是椭圆曲线数字签名算法？

ECDSA 执行与任何其他数字签名相同的函数，但效率更高。这样，ECDSA 与其他数字签名算法一样，可以使用更小的密钥提供相同的安全级别。ECDSA 用于创建 ECDSA 证书，这是一种用于验证证书所有者的电子文档。证书包含有关用于创建证书的密钥、证书所有者和发行者签名的信息，发行者签名是一个经过验证的可信实体。

这个可信的发行者通常是具有已签名证书的证书颁发机构，该证书可以通过信任链追溯到原始的发行者证书颁发机构。

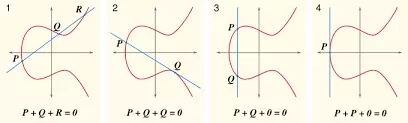
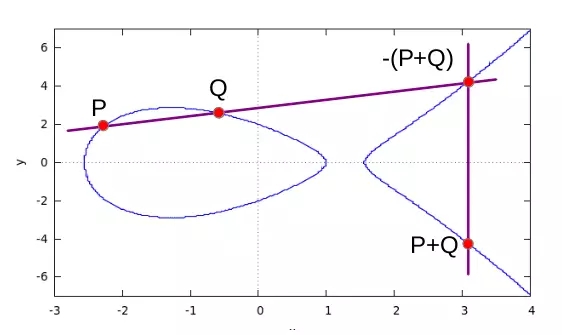
ECDSA 通过分析椭圆曲线并在曲线上选择一个点来操作。该点乘以另一个数，在曲线上产生一个新点。

即使原始点可用，也很难在曲线上找到新点。ECDSA 的复杂性意味着它比当前的加密破解方法更安全。除了对当前攻击方法更安全之外，ECDSA 还具有许多其他优点。

ECDSA Algorithm

密钥和签名大小

ECDSA 认为所需的私钥的位大小大约是安全级别（以位为单位）的两倍，这与一般的椭圆曲线密码学类似。例如，在 80 位的安全级别下，ECDSA 私钥的大小约为 160 位，这需要攻击者执行大约 280 次操作才能发现私钥。

但是，DSA 和 ECDSA 的签名大小相同：大约 4t 位，其中 t 是公式 2t 中的指数，用于 80 位安全级别，即大约 320 位，或 280 次操作。

签名生成

假设 Alice 想给 Bob 发送一条签名的消息。他们必须首先就曲线的参数达成一致 (CURVE, G, n)。除了曲线的域和方程之外，还需要基点 G（曲线上素数阶的基点）；n 是点 G 的乘法阶。

参数

  • CURVE - 用于椭圆曲线的方程和域。
  • G - 椭圆曲线的基点；曲线上产生大素数阶子群 n 的一个点。
  • n - G 的整数阶，这表示 n x G = O，其中 O 是单位元。
  • dA - 随机选择的私钥。
  • QA - 公钥 dA x G（椭圆曲线计算）
  • m - 要传输的文本

起点 G 的阶 n 必须是素数。事实上，Z/nZ 必须是一个域，因为我们假设环的每个非零元素都是可逆的。这意味着 n 必须是一个素数。

Alice 生成一对密钥，包括公钥曲线点 QA = dA x G 和私钥整数 dA，后者是从区间 [1, n-1] 中随机选择的。标量的椭圆曲线点乘法用符号 x 表示。

签名消息

Alice 为了签名消息执行以下步骤：

  • 确定 e = HASH(m)。（这里，HASH 指的是将输出转换为整数的密码哈希算法，例如 SHA-2。）
  • 令 z 表示 e 的最左边的 Ln 位，其中 Ln 表示群阶 n 的位长度。（请注意，z 不长于 n，尽管它可以是。）
  • 选择 k，一个来自 [1, n-1] 的密码安全的随机整数。
  • 计算曲线点，其中 k x G = (x1, y1) = 0。
  • 通过取 x1 mod n 来计算 r。如果 r = 0，请参考步骤 3。
  • 必须计算 S = k-1 (z + rdA) mod n。如果 s = 0，请参考步骤 3。
  • 这对 (r, s) 就是签名。此外，(r, -s mod n) 也是有效的签名。

如果 k 由不可靠的随机数生成器产生，则 ECDSA 签名可能会泄露私钥的另一种方法。2013 年 8 月，Android 比特币钱包的用户由于随机数生成错误而损失了资金。

您可以通过从消息和私钥派生 k 来生成确定性签名，从而完全避免随机数的创建，并确保 k 对于每次通信都是唯一的。

使用 Python 实现 ECDSA

基本上，我们将使用 Python 的 ecdsa 库，它提供了处理 ECDSA 算法的功能。我们还将使用 hashlib 库将给定的消息转换为哈希形式。以下是使用 ecdsa 和 haslib 库的 ECDSA 的简单 Python 实现：

示例

from ecdsa import SigningKey, VerifyingKey, SECP256k1
import hashlib

# Create a new private key
private_key = SigningKey.generate(curve=SECP256k1)

# Derive the public key from the private key
public_key = private_key.verifying_key

# Some message to sign
message = b"Hello, Tutorialspoint!"

# Hash the message
hash_message = hashlib.sha256(message).digest()

# Sign the hashed message with the private key
signature = private_key.sign(hash_message)

# Verify the signature using the public key
is_valid = public_key.verify(signature, hash_message)

if is_valid:
   print("Signature is valid.")
else:
   print("Signature is not valid.")

以下是上述示例的输出：

输入/输出

运行以上代码需要安装Python的hashlib和ecdsa库。可以使用`pip install 'libraryName'`安装这些库。将代码保存到文件中，然后使用`python ecdsa_implement.py`运行此代码。这里我们的文件名是ecdsa_implement.py。文件的输出如下：

Signature is valid.

ECDSA的安全性

虽然RSA是一种非常安全的加密方法，但ECC可能更有效。

理论上，量子计算机可以通过有效解决RSA的基础——因式分解问题来破解RSA。关于这何时会发生存在很多争议。但可以肯定的是，与RSA相比，由于其复杂性，ECC对量子计算攻击更具抵抗力。

抵抗力有多强？在一篇研究论文中，一位荷兰数学家将破解加密方法比作烧水。目标是确定破解特定加密算法所需的能量以及可以用该能量烧开的开水量。

换句话说，破解228位ECC密钥可以烧开地球上所有的水，而破解228位RSA密钥所需的能量却比烧开一茶匙水还要少。要达到与RSA相同的安全级别，需要2380位的密钥大小。

ECDSA的弱点

根据现有信息，椭圆曲线数字签名算法的弱点分析如下：

  • 实现复杂性 - ECDSA 的正确实现比 RSA 更困难，这可能会增加实现错误的可能性。实现不当的椭圆曲线数字签名算法可能会危及安全性。
  • 输出长度 - 对于相同的安全级别，ECDSA 比 RSA 产生的输出长度更短。3072 位 RSA 签名等于 256 位 ECDSA 签名的安全级别。较短的输出长度可能会使 ECDSA 签名更容易受到暴力攻击。
  • 椭圆曲线的选择 - 椭圆曲线很重要，因为某些曲线允许攻击者进行暴力破解加密。选择能够防止攻击者找到离散对数问题的多项式时间实现的椭圆曲线至关重要。
  • 扭曲攻击 - “扭曲攻击”是一种潜在的弱点，攻击者向消息接收者发送一组精心选择的椭圆曲线点进行加密。如果消息接收者的算法实现不当，攻击者可能会能够从密文中提取私钥。
  • 安全性与实现复杂性 - ECDSA 的实现难度会影响其安全性。确保安全实现对于避免漏洞至关重要。

ECDSA 的用途

  • 安全的通信协议 - ECC 用于许多安全的通信协议中，以实现加密、数字签名和密钥交换。例如，用于安全网络通信的虚拟专用网络 (VPN)，用于安全远程登录的安全外壳 (SSH) 以及用于安全在线浏览的传输层安全 (TLS)。
  • 区块链技术和加密货币 - 比特币、以太坊和莱特币等多种加密货币使用椭圆曲线密码学来创建公钥和私钥对以及签名交易。ECC 提供了保护数字资产和保证区块链网络完整性所需的加密保护。
  • 智能卡和嵌入式系统 - ECC 常用于保护电子护照、支付系统、访问控制系统以及其他需要小型安全加密解决方案的应用程序。
ECDSA Usage

ECDSA 的优点

  • 2005 年制定了新的标准。
  • 标准化减少了黑客时间，因此时间更短。
  • 其复杂性和新颖性使其不易受到攻击。
  • 对于新兴的公钥密码学协议来说是一个理想的替代方案。

ECDSA 的缺点

  • 实现复杂，可能导致错误的实现。
  • RSA 于 1995 年标准化，拥有更悠久的历史。
  • 由于其悠久的历史，RSA 仍然是最广泛使用的方法。
  • RSA 更易于设置，部署障碍更少。
打印页面
上一篇
下一篇
广告