自定义构建密码算法（混合密码学）

上一页
下一页

混合密码学结合了两种或多种加密技术。它结合了非对称加密和对称加密，以利用各自的功能。该方案使用公钥密码学来共享密钥，并使用对称加密来高效地加密消息。

混合加密方案结合了非对称加密方法的优点和对称加密方法的有效性。

要加密消息，首先生成一个对称密钥。然后，想要向其发送消息的人共享她的公钥，同时保持私钥私密。之后，使用接收者的公钥加密对称密钥并将其传输给他们。

要解密通信，接收者使用她的私钥解密加密的对称密钥以获得解密密钥，然后她使用该密钥来解码消息。

查看下面的图片以直观地了解混合密码学

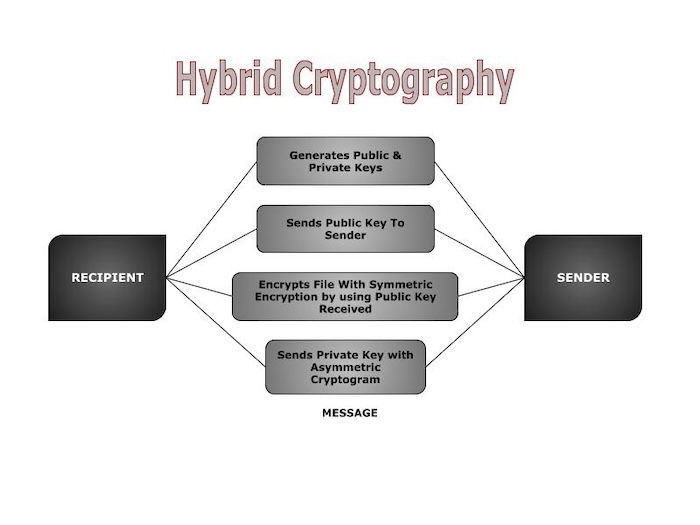
Hybrid Cryptography

以下是我们在上图中提到的步骤的解释：

  • 生成公钥和私钥 - 接收者首先创建一对密钥：公钥和私钥。
  • 将公钥发送给发送者 - 接收者将其公钥发送给发送者。公钥可以公开分发，因为它仅用于加密。
  • 使用接收到的公钥通过对称加密加密文件 - 发送者希望安全地将文件发送给接收者。发送者在使用对称加密加密文件的同时，也使用了接收者的公钥。这意味着只有拥有相应私钥的接收者才能解密文件。
  • 使用非对称密码发送私钥 - 发送者现在将把接收者的私钥发送给他，但它是使用非对称加密加密的。此加密的私钥确保只有拥有相应私钥的预期接收者才能解密它。

混合密码学的实现

我们将借助不同的编程语言（如 Python、Java 和 C++）来实现混合密码学。因此，请参考以下部分的代码：

使用 Python

此实现中的自定义加密基于移动连接密钥中每个字符的 ASCII 值。对于偶数索引的字符，每个字符都按公钥的长度移动，对于奇数索引的字符，每个字符都按对称密钥的长度移动。这是一种简单的加密类型，它仍然使用组合密钥和应用自定义转换的方法。因此，请参见下面的 Python 实现：

def hybrid_encrypt(message, public_key, symmetric_key):
   # Reverse the message
   reversed_message = message[::-1]
   # Combine reversed message with symmetric key
   combined_key = reversed_message + symmetric_key

   # change combined key to list of characters
   key_characters = list(combined_key)

   # Apply custom encryption
   encrypted_characters = []
   for i, char in enumerate(key_characters):
      if i % 2 == 0:
         encrypted_char = chr(ord(char) + len(public_key))  # Shift ASCII value by length of public key
      else:
         encrypted_char = chr(ord(char) - len(symmetric_key))  # Shift ASCII value by length of symmetric key
         encrypted_characters.append(encrypted_char)

   # Combine encrypted characters 
   encrypted_message = ''.join(encrypted_characters)

   return encrypted_message

# our message, public key and symmetric key
message = "hellotutorialspoint"
public_key = "qwer"
symmetric_key = "private"

# function execution

encrypted_message = hybrid_encrypt(message, public_key, symmetric_key)
print("Our Encrypted Message:", encrypted_message)

输出

Our Encrypted Message: xgmhtlpZmksmymsep^livbzZx^

使用 Java

此 Java 程序演示了使用给定密钥对明文消息应用的混合加密技术。main 方法初始化明文消息和密钥，然后调用 encryptMessage 函数来加密明文。

import java.util.*;

class HybridEncryption {

   public static void main(String[] args) {
      String plaintext = "hellotutorialspoint";
      String key = "qwer";
      System.out.println("Our Encrypted Message is: " + encryptMessage(plaintext, key));
   }

   public static String encryptMessage(String message, String key) {
      int a = 0, b = 1, c = 0, m = 0, k = 0, j = 0;
      String encryptedText = "", temp = "";

      // Reverse the message
      StringBuilder reversedMessage = new StringBuilder(message).reverse();
      // Combine the reversed message with the key
      StringBuilder combinedString = reversedMessage.append(key);

      // change the combined string to a character array
      char[] charArray = combinedString.toString().toCharArray();
      String evenChars = "", oddChars = "";

      // Separate characters into even and odd positions
      for (int i = 0; i < charArray.length; i++) {
         if (i % 2 == 0) {
            oddChars += charArray[i];
         }else {
            evenChars += charArray[i];
         }
      }

      char[] evenArray = new char[evenChars.length()];
      char[] oddArray = new char[oddChars.length()];

      // create a Fibonacci series and apply Caesar cipher
      while (m <= key.length()) {
         if (m == 0)
            m = 1;
         else {
            a = b;
            b = c;
            c = a + b;
            for (int i = 0; i < evenChars.length(); i++) {
               int p = evenChars.charAt(i);
               int cipher = 0;
               if (Character.isDigit(p)) {
                  cipher = p - c;
                  if (cipher < '0')
                     cipher = cipher + 9;
               }else {
                  cipher = p - c;
                  if (cipher < 'a') {
                     cipher = cipher + 26;
                  }
               }
               evenArray[i] = (char)cipher;
            }
            for (int i = 0; i < oddChars.length(); i++) {
               int p = oddChars.charAt(i);
               int cipher = 0;
               if (Character.isDigit(p)) {
                  cipher = p + c;
                  if (cipher > '9')
                     cipher = cipher - 9;
               }else {
                  cipher = p + c;
                  if (cipher > 'z') {
                     cipher = cipher - 26;
                  }
               }
               oddArray[i] = (char)cipher;
            }
            m++;
         }
      }

      // Combine even and odd characters based on their positions
      for (int i = 0; i < charArray.length; i++) {
         if (i % 2 == 0) {
            charArray[i] = oddArray[k];
            k++;
         }else {
            charArray[i] = evenArray[j];
            j++;
         }
      }
      // Generate the encrypted text
      for (char d : charArray) {
         encryptedText = encryptedText + d;
      }

      // Return the encrypted text
      return encryptedText;
   }
}

输出

Our Encrypted Message is: wkllspoxlorqxqriobknzbu

使用 C++

此 C++ 代码显示了一种自定义加密算法，该算法结合了反向字符串操作和凯撒密码来加密消息。

#include <iostream>
#include <string>
#include <algorithm> // Include the algorithm header for the reverse function

using namespace std;

string hybridEncryption(string password, string key) {
   int a = 0, b = 1, c = 0,
      m = 0, k = 0, j = 0;
   string cipherText = "", temp = "";

   // Declare a password string
   string reversedPassword = password;

   // Reverse the String
   reverse(reversedPassword.begin(), reversedPassword.end()); // Use the reverse function
   reversedPassword = reversedPassword + key;

   // For future Purpose
   temp = reversedPassword;
   string charArray = temp;
   string evenChars = "", oddChars = "";

   // Declare EvenArray for storing
   // even index of charArray
   char *evenArray;

   // Declare OddArray for storing
   // odd index of charArray
   char *oddArray;

   // Storing the positions in their
   // respective arrays
   for (int i = 0; i < charArray.length(); i++) {
      if (i % 2 == 0) {
         oddChars = oddChars + charArray[i];
      }else {
         evenChars = evenChars + charArray[i];
      }
   }

   evenArray = new char[evenChars.length()];
   oddArray = new char[oddChars.length()];

   // Generate a Fibonacci Series
   // Upto the Key Length
   while (m <= key.length()) {

      // As it always starts with 1
      if (m == 0)
         m = 1;

      else {

         // Logic For Fibonacci Series
         a = b;
         b = c;
         c = a + b;

         for (int i = 0; i < charArray.length(); i++) {

            // Caesar Cipher Algorithm Start
            // for even positions
            int p = charArray[i];
            int cipher = 0;

            if (p == '0' || p == '1' ||
               p == '2' || p == '3' ||
               p == '4' || p == '5' ||
               p == '6' || p == '7' ||
               p == '8' || p == '9') {
               cipher = p - c;

               if (cipher < '0')
                  cipher = cipher + 9;
            }else {
               cipher = p - c;
               if (cipher < 'a') {
                  cipher = cipher + 26;
               }
            }
            evenArray[i] = (char)cipher;

            // Caesar Cipher Algorithm End
         }
         for (int i = 0; i < charArray.length(); i++) {

            // Caesar Cipher Algorithm
            // Start for odd positions
            int p = charArray[i];
            int cipher = 0;

            if (p == '0' || p == '1' ||
               p == '2' || p == '3' ||
               p == '4' || p == '5' ||
               p == '6' || p == '7' ||
               p == '8' || p == '9') {
                  cipher = p + c;
                  if (cipher > '9')
                     cipher = cipher - 9;
            }else {
               cipher = p + c;
               if (cipher > 'z') {
                  cipher = cipher - 26;
               }
            }
            oddArray[i] = (char)cipher;

            // Caesar Cipher Algorithm End
         }
         m++;
      }
   }

   // Storing content of even and
   // odd array to the string array
   for (int i = 0; i < charArray.length(); i++) {
      if (i % 2 == 0) {
         charArray[i] = oddArray[k];
         k++;
      }else {
         charArray[i] = evenArray[j];
         j++;
      }
   }

   // Generating a Cipher Text
   // by charArray (Caesar Cipher)
   for (char d : charArray) {
      cipherText = cipherText + d;
   }

   // Return the Cipher Text
   return cipherText;
}

// Driver code
int main() {
   string pass = "hellotutorialspoint";
   string key = "qwer";

   cout <<"Our Encrypted Message is: "<< hybridEncryption(pass, key);

   return 0;
}

输出

Our Encrypted Message is: wqqklfrlsmvpoidxlfuorlw

混合密码学的优点

混合加密是对称加密和非对称加密的组合，它比以前的方法提供了更高的安全性。数据的传输变得安全。在传输过程中加密数据可以提供安全优势，就像所有设备上都能确保数据安全一样。

打印页面
上一页
下一页
广告
© . All rights reserved.